Question

The line $\dfrac{x}{a}+\dfrac{y}{b}=1$ meets the axis of x and y at A and B respectively and the line $y=x$ at C so that area of the triangle AOC is twice the area of the triangle BOC, O being the origin, then one of the position of C is:
(a) $\left( a,a \right)$
(b) $\left( \dfrac{2a}{3},\dfrac{2a}{3} \right)$
(c) $\left( \dfrac{b}{3},\dfrac{b}{3} \right)$
(d) $\left( \dfrac{2b}{3},\dfrac{2b}{3} \right)$

Answer 1

Hint: Find the coordinates where the line $\dfrac{x}{a}+\dfrac{y}{b}=1$ meets the coordinate axis. Draw a suitable diagram with these points and apply the area condition mentioned in the question. Area of a triangle can be found using $\dfrac{1}{2}\times base\times height$.

Given that the line $\dfrac{x}{a}+\dfrac{y}{b}=1$meets the x axis at A and y axis at B.
Now, for point A:
Let us put $y=0$, in the line $\dfrac{x}{a}+\dfrac{y}{b}=1$
$\dfrac{x}{a}+\dfrac{0}{b}=1$
$x=a$
So, Point A is $\left( a,0 \right)$.
For point B:
Let us put $x=0$in the line $\dfrac{x}{a}+\dfrac{y}{b}=1$
$\dfrac{0}{a}+\dfrac{y}{b}=1$
$y=b$
So, Point B is $\left( 0,b \right)$.
Therefore, we can plot the below diagram with the data we obtained.

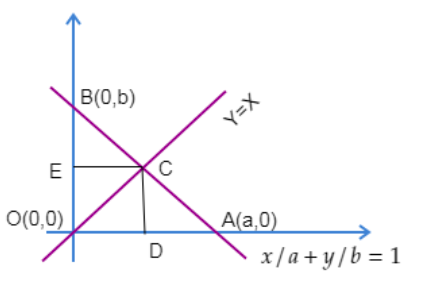
Now let us assume point C as $\left( m,m \right)$since it lies on the line $x=y$.
As mentioned in the question we have:
(Area of $\vartriangle AOC$) = 2(Area of $\vartriangle BOC$)
$\dfrac{1}{2}\times \left( OA \right)\left( CD \right)=2\times \dfrac{1}{2}\left( OB \right)\left( CE \right)$
Since, area of triangle = $\dfrac{1}{2}\times base\times height$.
We have:
$OA=a$
$CD=m$
$OB=b$
$CE=m$
Substituting the above values in $\dfrac{1}{2}\left( a \right)\left( m \right)=\left( b \right)\left( m \right)$, we will have:
$\therefore \dfrac{1}{2}\left( a \right)\left( m \right)=\left( b \right)\left( m \right)$
$a=2b$
Now let us substitute $a=2b$ in the line $\dfrac{x}{a}+\dfrac{y}{b}=1$
$\dfrac{x}{2a}+\dfrac{y}{b}=1...........(1)$
Substituting $c\left( m,m \right)$ in the equation (1), we will have:
$\dfrac{m}{2b}+\dfrac{m}{b}=1$
$3m=2b$
$m=\dfrac{2b}{3}$
Therefore, the coordinates of C can be $\left( \dfrac{2b}{3},\dfrac{2b}{3} \right)$.
Hence option D is the correct answer.

Note: We can also find the are of the triangle using the formula $\dfrac{1}{2}\left| {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right|$ when the three vertices of the triangle are known to us . But we adopt the formula of $\dfrac{1}{2}\times base\times height$ to save time.