Question

The line AB whose equation is x-y=2 cuts the x axis at A and B is (4,2). The line segment AB is rotated about A through an angle ${{45}^{\circ }}$ in the anticlockwise sense, then the equation AB in the new position is

& A.x=2 \\\ & B.x-1=0 \\\ & C.x-\sqrt{2}y-2=0 \\\ & D.y-2=0 \\\ \end{aligned}$$

Answer 1

For solving this question, we will first find slope of the given line. Then we will rotate the line by ${{45}^{\circ }}$ which will give us a value of $\theta$ which will give us a new slope of the line. Since coordinate A at x axis will remain same so we will find coordinate of A and then find equation of line using slope and coordinate of A. We will use following formula:
1: For finding a point on the x axis, put y = 0 and find the value of x. Point will be (x,0).
2: Slope of any line is given by $\tan \theta$ where $\theta$ is an angle formed by a line with x axis.
3: Slope of any line is given by $\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ where $\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)$ are any two points on lines.
4: Equation of a line having slope $\tan \theta$ and coordinate of any point as $\left( {{x}_{1}},{{y}_{1}} \right)$ is given by $\left( y-{{y}_{1}} \right)=\tan \theta \left( x-{{x}_{1}} \right)$.

Complete step-by-step answer:
Here we are given the equation of the line AB as $x-y=2\cdots \cdots \cdots \left( 1 \right)$.
Let us first find the coordinate of the point A.
Since point A cuts the x axis, so y coordinate will be zero.
Putting y = 0 in (1) we get,
$x-0=2\Rightarrow x=2$.
Hence A coordinate is (2,0).
Also point B is (4,2).
So two points of the line AB are (2,0) and (4,2)
We know slope ${{m}_{1}}$ any line passing through $\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)$ is given by ${{m}_{1}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ so we get:
${{m}_{1}}=\dfrac{2-0}{4-2}=\dfrac{2}{2}=1$.
Hence slope of line x-y=2 is 1.
Also as we know that, the slope of any line is $\tan \theta$ where $\theta$ is the angle that the line makes with the x axis. So we get $\tan \theta =1$.
As we know $\tan {{45}^{\circ }}=1$ so we get $\theta ={{45}^{\circ }}$.
Now line is rotated anticlockwise through an angle of ${{45}^{\circ }}$ so now $\theta$ becomes ${{45}^{\circ }}+{{45}^{\circ }}={{90}^{\circ }}$.

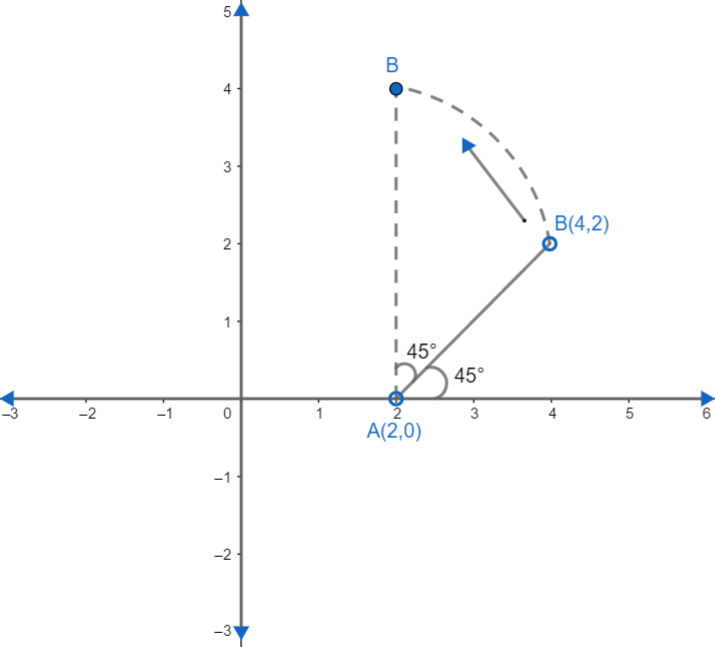
Hence $\theta ={{90}^{\circ }}$ for new lines. So the slope of the line becomes equal to $\tan {{90}^{\circ }}=\infty$. $\infty$ can also be written as $\dfrac{1}{0}$.
Now we know that, equation of line having slope m and passing through $\left( {{x}_{1}},{{y}_{1}} \right)$ is given by $\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)$.
Hence putting in $\left( {{x}_{1}},{{y}_{1}} \right)$ as (2,0) and m as $\dfrac{1}{0}$ we get:
$y-0=\dfrac{1}{0}\left( x-2 \right)\Rightarrow y=\dfrac{1}{0}\left( x-2 \right)$.
Cross multiplying we get:
$x-2=0\Rightarrow x=2$.
Hence x = 2 is the new equation of the line.

So, the correct answer is “Option A”.

Note: Students should always try to draw diagrams for understanding questions clearly. Take care of signs while forming the equation and while finding the coordinate of the point. Note that, if slope is $\dfrac{1}{0}$ then this means that line never touches the y axis.