Question
Question: The line AA’ is charged by an infinite conducting plane which is perpendicular to the plane of paper...
The line AA’ is charged by an infinite conducting plane which is perpendicular to the plane of paper. The plane has surface density of charge σand B is ball of mass m with a like charge of magnitude q. B is connected by string from a point on the line AA’ The tangent of angle (θ)formed between the line AA’ and the string is:
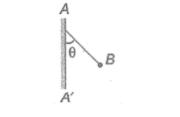
A.2ε0mgqσ B.2πε0mgqσ C.6πε0mgqσ D.ε0mgqσ
Solution
This problem can be solved by applying the concept of Gauss’s Law which states that, “The net electric flux through any hypothetical closed surface is equal to ε01 times the net electric charge within that closed surface.”
Complete step-by-step answer:
Step 1: Calculate the forces acting on the ball.
Let us draw the free-body diagram of the ball as follows:
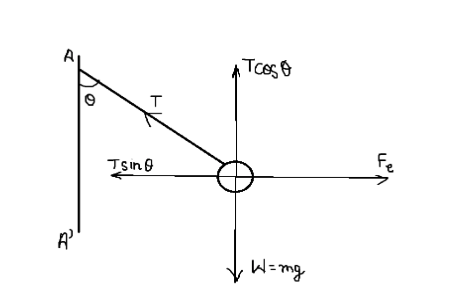
There are 3 forces acting on the ball: - Tension force, T due to the string. - Weight, W=mg acting downward. - Electric force, Fe due to the electric field due to an infinite plane.
The tension force can be resolved into 2 components as shown: Tsinθ&Tcosθ
To calculate electric force, Fe, we have to apply Gauss’s law for an infinite plane carrying charge density of σ.
Electric field due to infinite charge carrying plane, E=2ε0σ
Electric force,
Fe=qE Substituting, Fe=2ε0qσ
By equating the forces in the free-body diagram, we get two equations –
Tcosθ=mg Tsinθ=Fe
Dividing the equations –
TcosθTsinθ=mgFe tanθ=mgFe→(∵cosθsinθ=tanθ)
Substituting for Fe –
tanθ=mgFe tanθ=mg(2ε0qσ) tanθ=2ε0mgqσ
Hence, the correct option is Option A.
Note: Students generally confuse while writing the horizontal and vertical components of a vector. You can use a simple and handy thumb rule as shown here:

Consider a vector a inclined at angle θ as shown in the above figure: - The line that is attached to the angle θ is designated as cosθ. - The other line that is not attached to the angleθ is designated as sinθ
