Question
Question: The length of the tangent to the curve $x = a \left( \cos t + \log \tan \frac{t}{2} \right), y = a \...
The length of the tangent to the curve x=a(cost+logtan2t),y=asint is (where 0<t<4π)
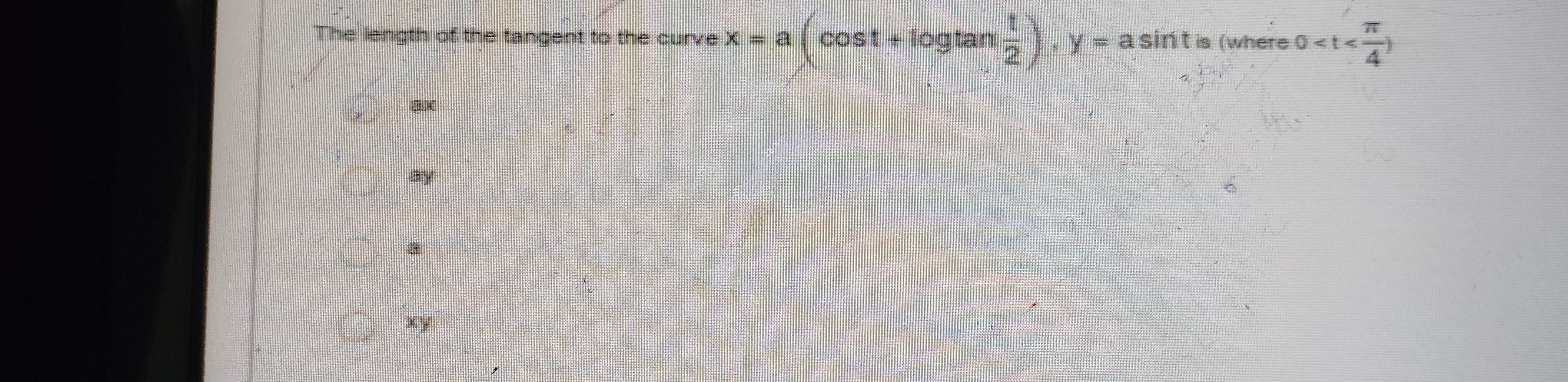
ax
ay
a
xy
a
Solution
The parametric equations of the curve are given by x=a(cost+logtan2t) and y=asint, where 0<t<4π.
First, we find the derivatives dtdx and dtdy. dtdx=dtd[a(cost+logtan2t)] dtdx=a(−sint+tan2t1⋅sec22t⋅21) Using tan2t=cos2tsin2t and sec22t=cos22t1, we get: dtdx=a(−sint+sin2tcos2t⋅cos22t1⋅21) dtdx=a(−sint+2sin2tcos2t1) Using the double angle formula sint=2sin2tcos2t, we have: dtdx=a(−sint+sint1)=a(sint1−sin2t)=asintcos2t.
dtdy=dtd(asint)=acost.
The slope of the tangent to the curve at parameter t is dxdy=dx/dtdy/dt. dxdy=asintcos2tacost=cos2tcostsint=costsint=tant.
Let the point of tangency be (x,y). The equation of the tangent line at this point is Y−y=dxdy(X−x), which is Y−y=tant(X−x).
The "length of the tangent" usually refers to the length of the segment of the tangent line from the point of tangency to its intersection with the x-axis or the y-axis. Let's calculate both.
-
Length of the tangent segment from (x,y) to the x-axis: The tangent intersects the x-axis when Y=0. 0−y=tant(X−x) −y=tant(X−x) X−x=−tanty=−ycott X=x−ycott. The intersection point is (x−ycott,0). The length of the tangent segment Lx is the distance between (x,y) and (x−ycott,0). Lx=((x−ycott)−x)2+(0−y)2=(−ycott)2+(−y)2 Lx=y2cot2t+y2=y2(cot2t+1)=y2csc2t=∣ycsct∣. Substitute y=asint: Lx=∣asint⋅csct∣=∣asint⋅sint1∣=∣a∣. Since a is a scale factor representing length, it is usually taken as positive. So, Lx=a.
-
Length of the tangent segment from (x,y) to the y-axis: The tangent intersects the y-axis when X=0. Y−y=tant(0−x) Y−y=−xtant Y=y−xtant. The intersection point is (0,y−xtant). The length of the tangent segment Ly is the distance between (x,y) and (0,y−xtant). Ly=(0−x)2+((y−xtant)−y)2=(−x)2+(−xtant)2 Ly=x2+x2tan2t=x2(1+tan2t)=x2sec2t=∣xsect∣. Substitute x=a(cost+logtan2t): Ly=a(cost+logtan2t)sect=a(costcost+costlogtan2t)=a(1+costlogtan2t). This expression does not simplify to one of the options ax,ay,a,xy.
Since one of the standard interpretations of "length of the tangent" (the length of the segment from the point of tangency to the x-axis) yields the result 'a', which is one of the options, this is likely the intended meaning of the question.
