Question

The length of the subtangent at $\left( {2,2} \right)$ to the curve ${x^5} = 2{y^4}$ is
A.$\dfrac{5}{2}$
B.$\dfrac{8}{5}$
C.$\dfrac{2}{5}$
D.$\dfrac{5}{8}$

Answer 1

In the given question, we have been given that there is a curve of degree 5, involving two variables raised to different powers. Then we have been given a reference point which has the same abscissa and ordinate. We have to calculate the length of the subtangent from the given reference point to the given curve. For solving this, we are going to first differentiate the given curve with respect to their respective variable terms, then put in the value of the given reference point and calculate the derivative at a given point. Then we are going to need to apply the formula of length of subtangent – divide the y-coordinate (or ordinate) of the given reference point by the calculated derivative at the reference point.

Complete step-by-step answer:
Given reference point, $P = \left( {2,2} \right)$

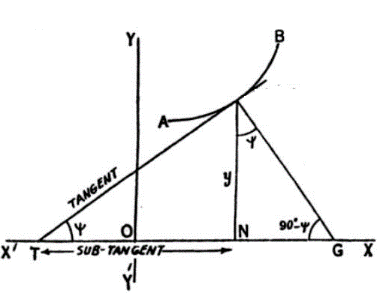
Given curve ${x^5} = 2{y^4}$
First, we are going to differentiate the curve with respect to $x$:
$\dfrac{{d\left( {{x^5}} \right)}}{{dx}} = \dfrac{{d\left( {2{y^4}} \right)}}{{dx}}$
$5{x^4} = 8{y^3}\dfrac{{dy}}{{dx}}$
Hence, ${\left( {\dfrac{{dy}}{{dx}}} \right)_{\left( {2,2} \right)}} = \dfrac{{5\left( {{2^4}} \right)}}{{8\left( {{2^3}} \right)}} = \dfrac{5}{4}$
Now, length of subtangent, $L = \dfrac{y}{{\left( {\dfrac{{dy}}{{dx}}} \right)}}$
Putting in the values and solving, $L = \dfrac{2}{{\dfrac{5}{4}}} = \dfrac{8}{5}$
Hence, the length of the subtangent is $\dfrac{8}{5}$.
Thus, the correct option is B.

Note: The length of tangent and subtangent are very different and their formulae are two very different expressions. But, the shifting of the variables in the formula of tangent and normal is the same as the shifting of the formula in tangent and subtangent. The pair of two formulae are kind of anomalous.