Question

The length of the simple pendulum has been found to be $1m$ and mass of its bob will be $50g$. The bob has been given required velocity such that the bob defines a vertical circle whose radius will be equivalent to the length of the pendulum. What will be the maximum difference in the kinetic energy of Bob during one revolution?
$\begin{aligned} & A.0.98J \\\ & B.1.96J \\\ & C.4.9J \\\ & D.9.8J \\\ \end{aligned}$

Answer 1

The velocity at the bottom will be equivalent to the square root of the product of the five, acceleration due to gravity and the radius of the path taken. The velocity at the top will be equivalent to the square root of the product of acceleration due to gravity and the radius. This will be helpful in answering this question.

Complete step by step solution:
First of all let us look at what all are given in the question,
The length of the simple pendulum has been given as,

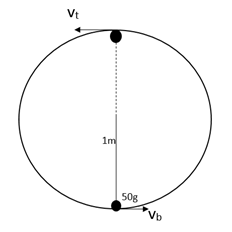
$L=1m$
Mass of the bob of the simple pendulum has been given as,
$m=0.05kg$
The centripetal force will be equivalent to the weight of the bob.
$\dfrac{m{{v}_{t}}^{2}}{R}=mg$
Where ${{v}_{t}}$ be the velocity at the top.
That is,
${{v}_{t}}=\sqrt{gR}$
Let ${{v}_{b}}$ be the minimum speed at the bottom then using equation of motion, we can write that,
${{v}_{b}}^{2}={{v}_{t}}^{2}+2gD$
That is,

& {{v}_{b}}^{2}=Rg+2g\times 2R=5gR \\\ & \Rightarrow {{v}_{b}}=\sqrt{5gR} \\\ \end{aligned}$$ The velocity at the bottom will be equivalent to the square root of the product of the five, acceleration due to gravity and the radius of the path taken. This can be written as, ${{V}_{b}}=\sqrt{5gR}$ The velocity at the top will be equivalent to the square root of the product of acceleration due to gravity and the radius. That is we can write that, ${{V}_{t}}=\sqrt{gR}$ The velocity will be maximum at bottom and the velocity will be minimum at the top. Therefore the change in kinetic energy can be written as, $\Delta KE=\dfrac{1}{2}m\left( {{\left( \sqrt{5gR} \right)}^{2}}-{{\left( \sqrt{gR} \right)}^{2}} \right)$ Simplifying the equation can be written as, $\Delta KE=\dfrac{1}{2}m\left[ 4gR \right]$ Substituting the values in the equation can be shown as, $\Delta KE=2\times \left( 0.05 \right)\times 9.8\times 1=0.98J$ Therefore the change in kinetic energy has been calculated. **The correct answer has been given as option A.** **Note:** The kinetic energy can be defined as the energy possessed by the body due to the motion of the body. The potential energy can be defined as the energy possessed by the body because of the orientation of the body. Both these energies can be expressed in the units of joule.