Question
Question: The length of the perpendicular from the point (0, 2, 3) on the line $\frac{x+3}{5} = \frac{y-1}{2} ...
The length of the perpendicular from the point (0, 2, 3) on the line 5x+3=2y−1= The equ
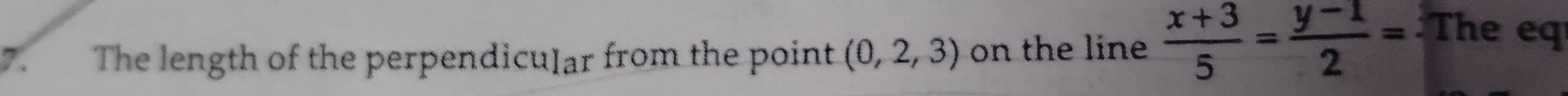
A
3059
Answer
3059
Explanation
Solution
We assume that the full equation of the line is
5x+3=2y−1=1z−1,so that a point on the line is
Q(−3,1,1)and its direction vector is
d=(5,2,1).Let the given point be
P(0,2,3).Then the vector from Q to P is
QP=P−Q=(0−(−3),2−1,3−1)=(3,1,2).The formula for the distance from a point to a line in 3D is
Distance=∥d∥∥QP×d∥.First, compute the cross product:
QP×d=i35j12k21=(1⋅1−2⋅2,2⋅5−3⋅1,3⋅2−1⋅5)=(−3,7,1).Its magnitude is
∥QP×d∥=(−3)2+72+12=9+49+1=59.Next, compute the magnitude of d:
∥d∥=52+22+12=25+4+1=30.Thus, the perpendicular distance is
Distance=3059=3059.