Question
Question: The length of the optical path of two media in contact of lengths \( {d_1} \) and \( {d_2} \) of ref...
The length of the optical path of two media in contact of lengths d1 and d2 of refractive indices μ1 and μ2 respectively is
\left( A \right){\mu _1}{d_1} + {\mu _2}{d_2} \\\
\left( B \right)\dfrac{{{\mu _1}{d_2} + {\mu _2}{d_1}}}{{{\mu _1}{\mu _2}}} \\\
\left( C \right)\dfrac{{{d_1}{d_2}}}{{{\mu _1}{\mu _2}}} \\\
\left( D \right)\dfrac{{{d_1} + {d_2}}}{{{\mu _1}{\mu _2}}} \\\
Solution
In order to solve this question, we are going to first see what an optical path actually is and then find the optical paths for the two mediums 1 and 2 respectively. Then, on adding the two refractive indices, we get the total optical path length of the two media in contact.
The optical path of a medium of refractive index μ and thickness t is given by
Optical path=μt
Complete step by step solution:
First of all let us see what an optical path means
The optical path can be defined as the product of the geometrical length of the original path followed by light through a given system and the refractive index of the medium through which it propagates.
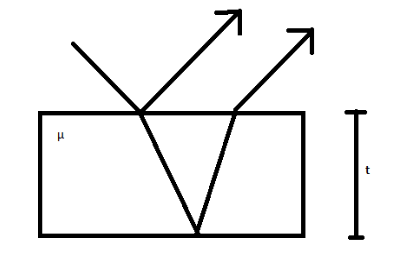
Optical path=μt
Where, μ is the refractive index
t is the thickness of the medium.
Thus, in medium 1, the thickness is d1 , so the optical path is
Optical path=μ1d1
In medium 2, the thickness is d2 , so the optical path is
Optical path=μ2d2
Now, to find the optical path of the two media, we will have to add the two optical paths as obtained above, thus, the optical path becomes
(Optical path)medium1+(Optical path)medium2
Therefore, the total length becomes
μ1d1+μ2d2
Hence, option (A)μ1d1+μ2d2 is the correct answer.
Note:
This is the optical path length and not to be confused with the optical path difference at any cost. The expression for the optical path difference is μ1d1−μ2d2 . This gives the difference for the two optical paths while for the total optical path, the two optical lengths are added for the final answer.
