Solveeit Logo
Login

Question

Question: The length of the normal chord to the parabola \[{y^2} = 4x\] which subtends a right angle at the ve...

The length of the normal chord to the parabola y2=4x{y^2} = 4x which subtends a right angle at the vertex is_____
A. 636\sqrt 3
B. 333\sqrt 3
C. 22
D. 11

Explanation

Solution

A line segment passing through any two points on the parabola is known as a chord, and the chord which is perpendicular to the tangent of the parabola at the point of intersection is known as a normal chord.

Complete step by step answer:

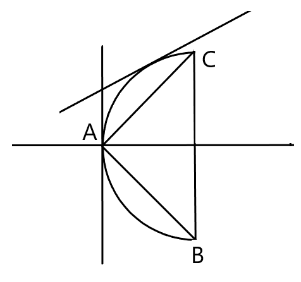
We are assuming CB as the chord to the parabola y2=4x{y^2} = 4x where a=1a = 1
Let \left( {a{t^2},2a{t_1}} \right)$$$$\left( {a{t_2}^2,2a{t_2}} \right) be the coordinates of C and B respectively. So, the equation becomes at point C,
y−2t1=−2t2(x−t2)y - 2{t^1} = \dfrac{{ - 2t}}{2}\left( {x - {t^2}} \right)
⇒y−2t1=−t(x−t2)\Rightarrow y - 2{t^1} = - t\left( {x - {t^2}} \right).................(equation 1)
Therefore, (slope of CA) (slope of AB)=−1 = - 1

As its given in the question, that the normal chord subtends a right angle at the vector
((2t−0)(t2−0))((2t2−0)(t22−0))=−1\left( {\dfrac{{\left( {2t - 0} \right)}}{{\left( {{t^2} - 0} \right)}}} \right)\left( {\dfrac{{\left( {2{t_2} - 0} \right)}}{{\left( {t_2^2 - 0} \right)}}} \right) = - 1
⇒(2tt2)(2t2t22)=−1\Rightarrow \left( {\dfrac{{2t}}{{{t^2}}}} \right)\left( {\dfrac{{2{t_2}}}{{t_2^2}}} \right) = - 1
⇒t1t2=−4\Rightarrow {t_1}{t_2} = - 4..................( equation 2)
From equation 2,
−t1(t2+t1)=2- {t_1}\left( {{t_2} + {t_1}} \right) = 2
⇒4−t12=2\Rightarrow 4 - t_1^2 = 2....................(equation 3)
⇒t1=2\Rightarrow t_1^{} = \sqrt 2

Substituting t1{t_1} in 3 equation = t2=−42{t_2} = \dfrac{{ - 4}}{{\sqrt 2 }}
⇒−422⇒−22\Rightarrow \dfrac{{ - 4\sqrt 2 }}{2} \Rightarrow - 2\sqrt 2
Coordinates of C= (2,22)\left( {2,2\sqrt 2 } \right)
Coordinates of B=(8,−42)\left( {8, - 4\sqrt 2 } \right)
Therefore the length of the normal chord is, here we are using the distance formula we can get the distance between the two coordinates C and B respectively.

\Rightarrow \sqrt {{6^2} + {{\left( { - 6\sqrt 2 } \right)}^2}} \\\ \Rightarrow \sqrt {108} \\\ \therefore 6\sqrt 3 $$ In the end we came to a conclusion that the answer is $$6\sqrt 3 $$ units. **So, option A is the correct option.** **Note:** In the above solution, distance formula has been used to calculate the distance between two coordinates given. It is an application of the Pythagorean theorem.Interestingly, a lot of people don't actually memorize this formula. Instead, they set up a right triangle, and use the Pythagorean theorem whenever they want to find the distance between two points.