Question

The length of the normal chord to the parabola, ${{y}^{2}}=4x$, which subtends a right angle at the vertex is,
(a). $6\sqrt{3}$
(b). $3\sqrt{3}$
(c). 2
(d). 1

Answer 1

- Hint: Draw figure of parabola, ${{y}^{2}}=4x$. Consider the point on the parabola as $\left( a{{t}^{2}},2at \right)$. Thus find the value of a and t, thus form the points of parabola and find the length of normal chord.

Complete step-by-step solution -

Let us consider PQ as the normal chord to the parabola, ${{y}^{2}}=4x$.

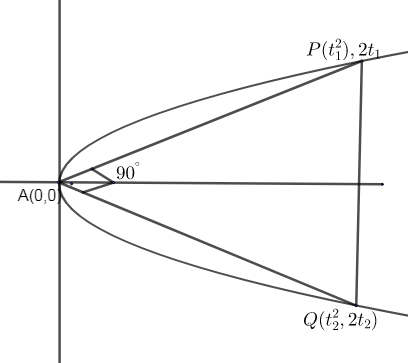
We know the general representation of a parabola is ${{y}^{2}}=4x$, where 4a is the latus rectum. By comparing both general equation and the given equation of parabola, we can say that,
4a = 4
Thus we get, a = 1.
Now let us consider point P as $\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)$ and Q $\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$. Thus putting a = 1, we get the coordinates as P $\left( {{t}_{1}}^{2},2{{t}_{1}} \right)$ and Q $\left( {{t}_{2}}^{2},2{{t}_{2}} \right)$.
The equation of the tangent to the normal is given by,
$y-{{y}_{1}}=\dfrac{-{{y}_{1}}}{2a}\left( x-{{x}_{1}} \right)$, where slope of the normal = $\dfrac{-{{y}_{1}}}{2a}$.
Thus equation of the normal at point P $\left( {{t}_{1}}^{2},2{{t}_{1}} \right)$ is,
Take, $\left( {{x}_{1}},{{y}_{1}} \right)=\left( t_{1}^{2},2{{t}_{1}} \right)$.

& y-2{{t}_{1}}=\dfrac{-2{{t}_{1}}}{2\times 1}\left( x-t_{1}^{2} \right) \\\ & \Rightarrow y-2{{t}_{1}}=-{{t}_{1}}\left( x-t_{1}^{2} \right)-(1) \\\ \end{aligned}$$ Now let us find the equation of normal at point Q $$\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$$. Take $$\left( {{x}_{1}},{{y}_{1}} \right)=\left( t_{1}^{2},2{{t}_{1}} \right)$$ and $$\left( x,y \right)=\left( t_{2}^{2},2{{t}_{2}} \right)$$. $$\begin{aligned} & 2{{t}_{2}}-2{{t}_{1}}=\dfrac{-2{{t}_{1}}}{2}\left[ t_{2}^{2}-t_{1}^{2} \right] \\\ & \Rightarrow 2\left( {{t}_{2}}-{{t}_{1}} \right)=-{{t}_{1}}\left( t_{2}^{2}-t_{1}^{2} \right) \\\ \end{aligned}$$ We know that, $${{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right)$$ $$\therefore 2\left( {{t}_{2}}-{{t}_{1}} \right)=-{{t}_{1}}\left( {{t}_{2}}-{{t}_{1}} \right)\left( {{t}_{2}}+{{t}_{1}} \right)$$ Cancel out $$\left( {{t}_{2}}-{{t}_{1}} \right)$$ from both sides. $$\therefore 2=-{{t}_{1}}\left( {{t}_{2}}+{{t}_{1}} \right)-(2)$$ Let us consider A as the vertex of the parabola. It is given that the normal chord subtends a right angle at the vertex A (0, 0). Thus we can say that $$PA\bot QA$$, from the figure. The perpendicular normal corresponds to the value that slope of PA and AQ will be (-1) i.e. $${{m}_{1}}{{m}_{2}}=-1$$. Thus we can say that, (slope of AP) (slope of AQ) = -1 Slope of AP = $${{m}_{1}}$$ Slope of AQ = $${{m}_{2}}$$ We can find the slope of a line using the formula, $$m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$$. Where, $$\left( {{x}_{1}},{{y}_{1}} \right)=\left( 0,0 \right)$$ and $$\left( {{x}_{2}},{{y}_{2}} \right)=\left( t_{1}^{2},2{{t}_{1}} \right)$$. $$\therefore $$ Slope of AP $$={{m}_{1}}=\dfrac{2{{t}_{1}}-0}{t_{1}^{2}-0}=\dfrac{2}{{{t}_{1}}}$$ Similarly, slope of AQ $$={{m}_{2}}=\dfrac{2{{t}_{2}}-0}{t_{2}^{2}-0}=\dfrac{2}{{{t}_{2}}}$$ $$\therefore $$ (slope of PA) (slope of AQ) = -1 $$\begin{aligned} & \therefore {{m}_{1}}{{m}_{2}}=-1 \\\ & \dfrac{2}{{{t}_{1}}}\times \dfrac{2}{{{t}_{2}}}=-1 \\\ & \Rightarrow 4=-{{t}_{1}}{{t}_{2}} \\\ \end{aligned}$$ i.e. $${{t}_{1}}{{t}_{2}}=-4-(3)$$ From equation (2) $$\Rightarrow 2=-{{t}_{1}}\left( {{t}_{2}}+{{t}_{1}} \right)$$ $$\Rightarrow 2=-{{t}_{1}}{{t}_{2}}-t_{1}^{2}$$ Put, $${{t}_{1}}{{t}_{2}}=4$$ $$\begin{aligned} & \Rightarrow 2=+4-t_{1}^{2} \\\ & \therefore t_{1}^{2}=2 \\\ & {{t}_{1}}=\sqrt{2} \\\ \end{aligned}$$ Now, $${{t}_{2}}=\dfrac{-4}{{{t}_{1}}}=\dfrac{-4}{\sqrt{2}}$$ [rationalizing, multiply by $$\sqrt{2}$$ on numerator and denominator] $${{t}_{2}}=\dfrac{-4\times \sqrt{2}}{\sqrt{2}\times \sqrt{2}}=\dfrac{-4\sqrt{2}}{2}=-2\sqrt{2}$$ $$\therefore {{t}_{1}}=\sqrt{2}$$ and $${{t}_{2}}=-2\sqrt{2}$$. Thus we get the coordinates of P and Q as, Coordinates of P $$=\left( {{\left( \sqrt{2} \right)}^{2}},2\sqrt{2} \right)=\left( 2,2\sqrt{2} \right)$$ Coordinates of Q $$=\left( {{\left( -2\sqrt{2} \right)}^{2}},-4\sqrt{2} \right)=\left( 8,-4\sqrt{2} \right)$$ Thus we got coordinates as P $$\left( 2,2\sqrt{2} \right)$$ and Q $$\left( 8,-4\sqrt{2} \right)$$. Thus we can find the length of a normal chord PQ by using distance formula. Distance $$=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$$ PQ $$=\sqrt{{{\left( 8-2 \right)}^{2}}+{{\left( -4\sqrt{2}-2\sqrt{2} \right)}^{2}}}$$ $$\left\\{ \begin{aligned} & \because \left( {{x}_{1}},{{y}_{1}} \right)=\left( 2,2\sqrt{2} \right) \\\ & \left( {{x}_{2}},{{y}_{2}} \right)=\left( 8,-4\sqrt{2} \right) \\\ \end{aligned} \right\\}$$ $$\begin{aligned} & PQ=\sqrt{{{6}^{2}}+{{\left( -6\sqrt{2} \right)}^{2}}}=\sqrt{36+72} \\\ & PQ=\sqrt{108}=\sqrt{6\times 6\times 3} \\\ & PQ=6\sqrt{3} \\\ \end{aligned}$$ Thus we got the length of the normal chord PQ as $$6\sqrt{3}$$. _$$\therefore $$ Option (a) is correct._ Note: The normal chord of parabola is any chord which is perpendicular to the axis of parabola. Here PA and QA are the lines which are perpendicular. The normal chord to parabola, whose ordinate is equal to abscissa subtends right angle at focus.