Question

The length of the latus rectum of the parabola whose vertex is (2, -3) and the directrix x = 4 is?
(a) 2
(b) 4
(c) 6
(d) 8

Answer 1

Consider the equation of the parabola in vertex form as ${{\left( y-k \right)}^{2}}=4a\left( x-h \right)$, where (h, k) is the vertex of the parabola. Substitute (x – h) = X and (y – k) = Y, write the equation as ${{Y}^{2}}=4aX$. Now, compare this equation of parabola with the form ${{y}^{2}}=4ax$ whose directrix is x = -a, substitute (x – h) in place of x for the relation of directrix. Find the values of ‘a’ and use the formula of latus rectum (L) of the parabola given as $L=4\left| a \right|$ to get the answer.

Complete step-by-step answer:
Here we have been provided with the coordinates of vertex and equation of the directrix of a parabola and we are asked to find the length of the latus rectum of this parabola.

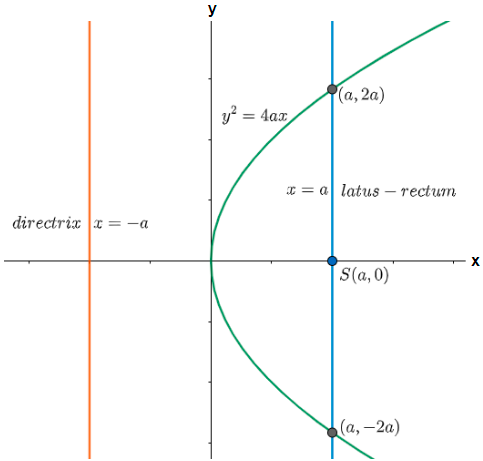
Now, the equation of a parabola with a vertex (h, k) other than the origin and directrix parallel to y axis is given by the standard form ${{\left( y-k \right)}^{2}}=4a\left( x-h \right)$. It is given that the vertex is (2, -3) so substituting the values of h and k in the equation we get,

& \Rightarrow {{\left( y-\left( -3 \right) \right)}^{2}}=4a\left( x-2 \right) \\\ & \Rightarrow {{\left( y+3 \right)}^{2}}=4a\left( x-2 \right) \\\ \end{aligned}$$ Substituting (x – 2) = X and (y + 3) = Y in the above equation we get the equation of the form ${{Y}^{2}}=4aX$. We can compare this equation with the equation of a parabola whose vertex lies on the origin given as ${{y}^{2}}=4ax$. The equation of the directrix of the parabola ${{y}^{2}}=4ax$ is given as x + a =0, so we can say that the equation of the directrix of the parabola ${{Y}^{2}}=4aX$ will be given as X + a = 0. Substituting the assumed value of X we get, $\begin{aligned} & \Rightarrow x-2+a=0 \\\ & \Rightarrow x=2-a \\\ \end{aligned}$ In the question we have been given that the equation of the directrix of the parabola is x = 4, so substituting the value of x in the above relation we get, $\begin{aligned} & \Rightarrow 4=2-a \\\ & \Rightarrow a=-2 \\\ \end{aligned}$ Therefore the equation of the parabola is $$\Rightarrow {{\left( y+3 \right)}^{2}}=4\left( -2 \right)\left( x-2 \right)$$. Now, we know that the length of the latus rectum (L) of a parabola ${{y}^{2}}=4ax$ is given as $L=4\left| a \right|$. Therefore, substituting the obtained valued of ‘a’ in the formula of length we get, $\begin{aligned} & \Rightarrow L=4\left| -2 \right| \\\ & \Rightarrow L=4\left( 2 \right) \\\ & \therefore L=8 \\\ \end{aligned}$ **So, the correct answer is “Option (d)”.** **Note:** Note that latus rectum of a parabola ${{y}^{2}}=4ax$ is a line parallel to the y – axis and passing through the focus S (a, 0) of the parabola. The coordinates of its end point is (a, 2a) and (a, -2a) lying in the first and fourth quadrant respectively. One thing you may conclude from the value of ‘a’, which is negative, in the above solution that the parabola will be opening leftward.