Question

The length of the latus rectum of the parabola whose focus is $(3,3)$ and directrix is $3x - 4y - 2 = 0$ is
(A) 2
(B) 1
(C) 4
(D) None

Answer 1

Hint : Find the perpendicular distance from $(3,3)$ to the line $3x - 4y - 2 = 0$ using the formula $d = \dfrac{{\left| {A(a) + B(b) + C} \right|}}{{\sqrt {{A^2} + {B^2}} }}$ . Multiply the distance by 2 to get the answer.

Complete step-by-step answer :
We are given the focus of a parabola $(3,3)$ and the equation of its directrix $3x - 4y - 2 = 0$ .
We are asked to find the length of the latus rectum of the parabola.

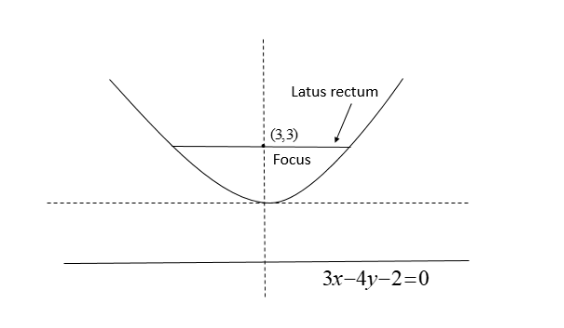
We know that the length of the latus rectum of the parabola is twice the perpendicular distance from the focus on to the directrix.
So, we need to find the perpendicular distance from the point $(3,3)$ to the line given by the equation $3x - 4y - 2 = 0$ .
The perpendicular distance from a point $(a,b)$ to the line $Ax + By + C = 0$ is given by the formula
$d = \dfrac{{\left| {A(a) + B(b) + C} \right|}}{{\sqrt {{A^2} + {B^2}} }}$ .
We have $A = 3,B = - 4,C = - 2$ . Also $a = 3,b = 3$
On substituting, we get
$d = \dfrac{{\left| {3 \times 3 + ( - 4) \times 3 + ( - 2)} \right|}}{{\sqrt {{3^2} + {{( - 4)}^2}} }} = \dfrac{{\left| {9 - 12 - 2} \right|}}{{\sqrt {9 + 16} }} = \dfrac{5}{5} = 1$
Therefore, length of the latus rectum $= 2d = 2 \times 1 = 2$ .
Hence the answer is 2 units.

Note : 1) A parabola is a set of points which is equidistant from the focus and the directrix.
2) The latus rectum is a chord passing through the focus and parallel to the directrix. That is, its endpoints lie on the parabola.