Solveeit Logo
Login

Question

Question: The length of the intercept on y-axis, by circle whose diameter is the line joining the points \[\le...

The length of the intercept on y-axis, by circle whose diameter is the line joining the points (−4,3)and(12,−1)\left( { - {\rm{4}},{\rm{3}}} \right){\rm{ and }}\left( {{\rm{12}}, - {\rm{1}}} \right) is
A)323\sqrt 2
B)13\sqrt {13}
C)4134\sqrt {13}
D)None of these.

Explanation

Solution

Hint: First find the midpoint of 2 given points which will in turn become the center of the circle as 2 points are the endpoint of diameter. Find distance between 2 points center, any point to get the radius. As you know center and radius find the equation of circle. The y-intercept of the circle in the form of x2+y2+2gx+2fy+c=0 is 2f2−c{x^2} + {y^2} + 2gx + 2fy + c = 0{\text{ is 2}}\sqrt {{f^2} - c} .

Complete step by step solution:
The two given points of diameter are written as follows:
A(−4,3);B(12,−1){\rm{A}}\left( { - {\rm{4}},{\rm{3}}} \right);{\rm{ B}}\left( {{\rm{12}}, - {\rm{1}}} \right)
Let the center of the circle be O=(x,y)O = \left( {x,y} \right)point.
By above we can say the following statements:
x coordinate of the point denoted by A is given by -4.
x coordinate of the point denoted by B is given by 12.
x coordinate of the point denoted by O is given by x.
y coordinate of the point denoted by A is given by 3.
y coordinate of the point denoted by B is given by -1.
y coordinate of the point denoted by o is given by y.
The point O is the midpoint of points A, B.
The x coordinate of O is average of x coordinates of A, B, we get:
x= average of - 4, 12 = 12−42x = {\text{ average of - 4, 12 = }}\dfrac{{12 - 4}}{2}
By simplifying we get the value of x to be as:
x=4x = 4
The y coordinate of O is average of y coordinates of A, B, we get:
y= average of 3, - 1 = 3−12y = {\text{ average of 3, - 1 = }}\dfrac{{3 - 1}}{2}
By simplifying we get the value of y to be as:
y=1y = 1
So, the center of circle is given by point O (4,1)\left( {{\rm{4}},{\rm{1}}} \right)

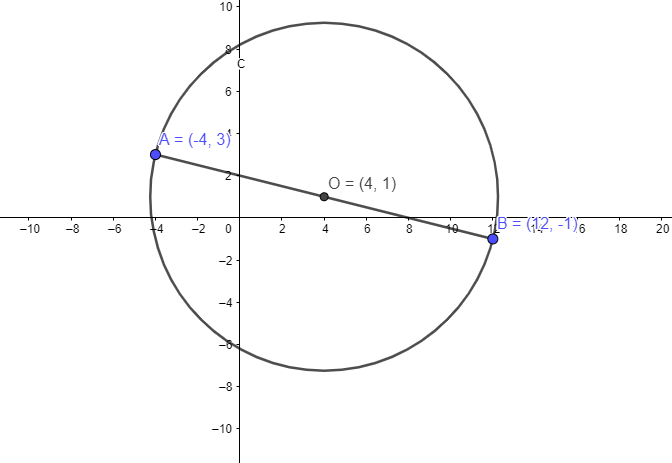
The radius of the circle can be denoted as OA.
The distance between two points (a, b) (c, d) is d, can be given by:
d=(a−c)2+(b−d)2d = \sqrt {{{\left( {a - c} \right)}^2} + {{\left( {b - d} \right)}^2}}
By substituting the values, we can write value of radius as:
Radius = distance between (4,1),(−4,3)=(4+4)2+(3−1)2\left( {4,1} \right),\left( { - 4,3} \right) = \sqrt {{{\left( {4 + 4} \right)}^2} + {{\left( {3 - 1} \right)}^2}}
By simplifying the above equation we can get value of radius as:
Radius =82+22=64+4=68= \sqrt {{8^2} + {2^2}} = \sqrt {64 + 4} = \sqrt {68}
Center =(4,1) = \left( {{\rm{4}},{\rm{1}}} \right)
If center is (g, f) and radius r, we get equation as:
(x−g)2+(y−f)2=r2{\left( {x - g} \right)^2} + {\left( {y - f} \right)^2} = {r^2}
By substituting the values, we get it as:
(x−4)2+(y−1)2=68{\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} = 68
By substituting (a−b)2=a2+b2−2ab,{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab,we get the equation as:
x2+16−8x+y2+1−2y=68{x^2} + 16 - 8x + {y^2} + 1 - 2y = 68
By simplifying the above equation, we get final equation as:
x2+y2−8x−2y−51=0{x^2} + {y^2} - 8x - 2y - 51 = 0
By comparing it to x2+y2+2gx+2fy+c=0{x^2} + {y^2} + 2gx + 2fy + c = 0, we get:
2g=−8,2f=−2⇒g=−4,f=−1,c=−512g = - 8,2f = - 2{\rm{ }} \Rightarrow {\rm{g = - 4,f = - 1,c = - 51}}
We know he y intercept given by:
y-intercept=2f2−c\text{y-intercept=2}\sqrt{{{f}^{2}}-c}
By substituting f, c values, we get it as:
y-intercept=21−(−51)=252\text{y-intercept=2}\sqrt{1-\left( -51 \right)}=2\sqrt{52}
52 can be written as 13×413 \times 4. So, by substituting it we get it as:
y intercept =413.= 4\sqrt {13.}
Therefore, option (c) is the correct answer.

Note: Be careful while getting the center as the whole equation of circle depends on that point. Don’t confuse between x, y coordinates. Alternate method is to substitute x=0{\rm{x}} = 0 and get the y values of the circle. Now get 2 intersection points on the y-axis. The distance between the two points is called the y-intercept. Anyway you get the same result.