Question

The length of the intercept made by the circle ${x^2} + {y^2} = 1$ on the line $x + y = 1$ is:-
(A) $\dfrac{1}{{\sqrt 2 }}$
(B) $\sqrt 2$
(C) 2
(D) $2\sqrt 2$

Answer 1

We will first find the points of intersection of line and circle by solving the equations. The length of intercept will be the distance between the points of intersection. We can calculate the distance between two points using the distance formula, $\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$, where $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ are coordinates of two points.

Complete step-by-step answer:
We have to find the length of the intercept made by the circle ${x^2} + {y^2} = 1$ on the line $x + y = 1$ is
We will first find the points of intersection of the circle ${x^2} + {y^2} = 1$ and the line $x + y = 1$.
From $x + y = 1$, we have $y = 1 - x$
We will substitute the value of $y$ in the equation of the circle.
${x^2} + {\left( {1 - x} \right)^2} = 1 \\\ \Rightarrow {x^2} + 1 + {x^2} - 2x = 1 \\\ \Rightarrow 2{x^2} - 2x = 0 \\\ \Rightarrow 2x\left( {x - 1} \right) = 0 \\\$
Equate each factor to 0 to find the value of $x$
$2x = 0 \\\ \Rightarrow x = 0 \\\$
And
$x - 1 = 0 \\\ \Rightarrow x = 1 \\\$
Now, we will substitute the value of $x$ to find the corresponding value of $y$.
When $x = 0$, then
$y = 1 - 0 \\\ \Rightarrow y = 1 \\\$
When $x = 1$, then,
$y = 1 - 1 \\\ \Rightarrow y = 0 \\\$
Hence, the coordinates of intercepts are $\left( {1,0} \right)$ and $\left( {0,1} \right)$.
We have to find the distance between these two points.

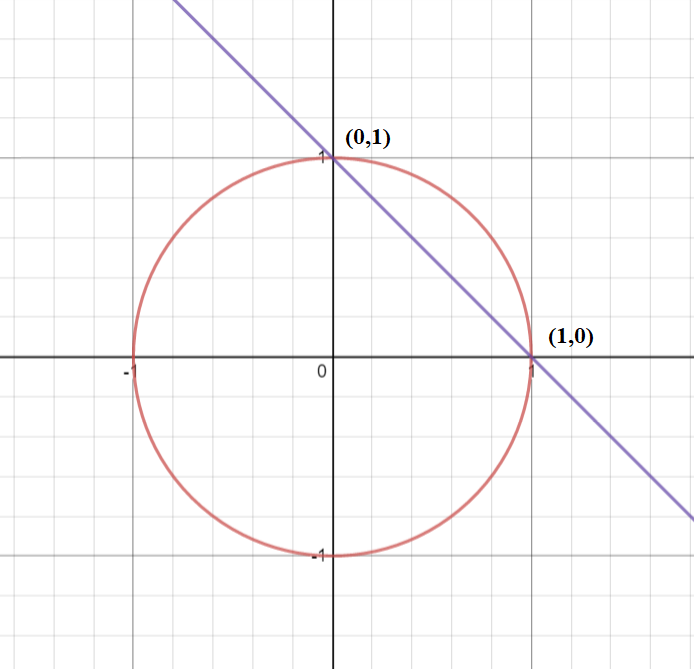
We know that if $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ are coordinates of two points, then the distance between them is given as $\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
Then, the length of intercept is
$\sqrt {{{\left( {1 - 0} \right)}^2} + {{\left( {0 - 1} \right)}^2}} = \sqrt {1 + 1} = \sqrt 2$
Hence, the length of the intercept made by the circle ${x^2} + {y^2} = 1$ on the line $x + y = 1$ is $\sqrt 2$ units.
Thus, option B is correct.

Note: Here, we can see that the equation of a circle ${x^2} + {y^2} = 1$ represents the circle of radius 1 unit and the points of coordinates of centre as $\left( {0,0} \right)$. We can also find the points of intersection of a given circle and line by plotting their graphs.