Solveeit Logo
Login

Question

Question: The length of the common chord of two circles \({\left( {x - a} \right)^2} + {\left( {y - b} \right)...

The length of the common chord of two circles (x−a)2+(y−b)2=c2 and (x−b)2+(y−a)2=c2{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {c^2}{\text{ and }}{\left( {x - b} \right)^2} + {\left( {y - a} \right)^2} = {c^2} is
A. 4c2+2(a−b)2\sqrt {4{c^2} + 2{{\left( {a - b} \right)}^2}}
B. 4c2+2(a+b)2\sqrt {4{c^2} + 2{{\left( {a + b} \right)}^2}}
C. 4c2−2(a−b)2\sqrt {4{c^2} - 2{{\left( {a - b} \right)}^2}}
D. c2−2(a−b)2\sqrt {{c^2} - 2{{\left( {a - b} \right)}^2}}

Explanation

Solution

Hint: If S1{S_1} is the equation of first circle and S2{S_2} is the equation of the second circle then the equation of common chord of both the circle is given as S1−S2=0{S_1} - {S_2} = 0 and the distance from the point (x1,y1)\left( {{x_1},{y_1}} \right) on the line ax−by=0ax - by = 0 is given as ∣ax1−bx2a2+b2∣\left| {\dfrac{{a{x_1} - b{x_2}}}{{\sqrt {{a^2} + {b^2}} }}} \right|.

Complete step by step answer:

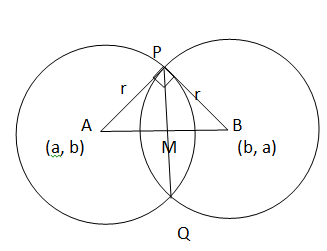
The equation of first circle is
S1=(x−a)2+(y−b)2=c2.............(1){S_1} = {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {c^2}.............\left( 1 \right)
And equation of the second circle is
S2=(x−b)2+(y−a)2=c2...............(2){S_2} = {\left( {x - b} \right)^2} + {\left( {y - a} \right)^2} = {c^2}...............\left( 2 \right)
Then the center of circle S1{S_1} is A (a, b) and radius is c.
The center of the circle of the circle S2{S_2} is B (b, a) and radius is c.
Now, PQ is a common chord AB intersect PQ at M and
AP=BP=c
Equation of PQ is given by,
S1−S2=0{S_1} - {S_2} = 0
⇒[(x−a)2+(y−b)2=c2 ] - [(x−b)2+(y−a)2=c2] ⇒2bx−2by+2ay−2ax=0 ⇒2b(x−y)+2a(y−x)=0 ⇒2b(x−y)−2a(x−y)=0 ⇒(x−y)(2b−2a)=0 ⇒x−y=0  \Rightarrow \left[ {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} = {c^2}{\text{ }}} \right]{\text{ - }}\left[ {{{\left( {x - b} \right)}^2} + {{\left( {y - a} \right)}^2} = {c^2}} \right] \\\ \Rightarrow 2bx - 2by + 2ay - 2ax = 0 \\\ \Rightarrow 2b\left( {x - y} \right) + 2a\left( {y - x} \right) = 0 \\\ \Rightarrow 2b\left( {x - y} \right) - 2a\left( {x - y} \right) = 0 \\\ \Rightarrow \left( {x - y} \right)\left( {2b - 2a} \right) = 0 \\\ \Rightarrow x - y = 0 \\\
Then equation of PQ is x−y=0x - y = 0
AM = length of perpendicular from A (a, b) on PQ whose equation is x−y=0x - y = 0
Therefore, AM =∣1×a−1×b∣(1)2+(−1)2=∣a−b∣2 = \dfrac{{\left| {1 \times a - 1 \times b} \right|}}{{\sqrt {{{\left( 1 \right)}^2} + {{\left( { - 1} \right)}^2}} }} = \dfrac{{\left| {a - b} \right|}}{{\sqrt 2 }}
In right ΔPMA,\Delta {\text{PMA,}}
PM=(AP)2−(AM)2 PM=c2−(a−b)22 [as AP = c (radius of the circle)]  PM = \sqrt {{{\left( {AP} \right)}^2} - {{\left( {AM} \right)}^2}} \\\ PM = \sqrt {{c^2} - \dfrac{{{{\left( {a - b} \right)}^2}}}{2}} \\\ \left[ {{\text{as AP = c }}\left( {{\text{radius of the circle}}} \right)} \right] \\\
But M is the midpoint of PQ
Then, PQ =2PM = 2
c2−(a−b)22 =4c2−4(a−b)22 =4c2−2(a−b)2  \sqrt {{c^2} - \dfrac{{{{\left( {a - b} \right)}^2}}}{2}} \\\ = \sqrt {4{c^2} - \dfrac{{4{{\left( {a - b} \right)}^2}}}{2}} \\\ = \sqrt {4{c^2} - 2{{\left( {a - b} \right)}^2}} \\\

Hence, the correct option is “C”.

Note: In order to solve these types of problems remember all the formulas and equations of lines and circles. Draw the diagram of the given problem; this helps in solving the problem and visualization of the problem. Be familiar with the terms like length of the perpendicular, foot of the perpendicular, chord, tangent and many more.