Question

The length of the common chord of two circles ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{c}^{2}}~$ and ${{\left( x-b \right)}^{2}}+{{\left( y-a \right)}^{2}}={{c}^{2~}}$ is
A) $\sqrt{4{{c}^{2}}+2{{\left( a-b \right)}^{2}}}$
B) $\sqrt{4{{c}^{2}}+2{{\left( a+b \right)}^{2}}}$
C) $\sqrt{4{{c}^{2}}-2{{\left( a-b \right)}^{2}}}$
D) $\sqrt{{{c}^{2}}+2{{\left( a-b \right)}^{2}}}$​

Answer 1

Here we to find the length of the common chord, we will first use the basic properties of chord of a circle and then we will use the Pythagoras theorem in triangle formed inside the circle which states that the square of longest side of a right angle triangle is equal to the sum of squares of other two sides of a triangle. From there, we will get the length of the common chord.

Complete step by step solution:
Let ${{S}_{1}}$ be the equation of the first circle and ${{S}_{2}}$ the equation of the second circle.
Therefore,
$\Rightarrow {{S}_{1}}={{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}-{{c}^{2}}=0~$
$\Rightarrow {{S}_{2}}={{\left( x-b \right)}^{2}}+{{\left( y-a \right)}^{2}}-{{c}^{2~}}=0$
We can see that the center of the first circle is $\left( a,b \right)$ and $\left( b,a \right)$ is the center of the second circle.
Now, we will draw the figure of two circles having a common chord.

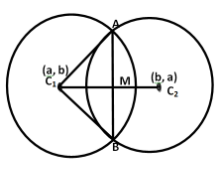
Equation of the common chord
$\Rightarrow {{S}_{1}}-{{S}_{2}}=0$
Now, we will substitute the equation of the first circle and the second circle.
$\Rightarrow {{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}-{{c}^{2}}-{{\left( x-b \right)}^{2}}-{{\left( y-a \right)}^{2}}+{{c}^{2~}}=0$
On expanding the terms using the algebraic identities, we get
$\Rightarrow {{x}^{2}}+{{a}^{2}}-2ax+{{y}^{2}}+{{b}^{2}}-2by-{{x}^{2}}-{{b}^{2}}+2bx-{{y}^{2}}-{{a}^{2}}+2ay=0$
On subtracting the like terms, we get the equation of the common chord as
$\Rightarrow -2ax-2by+2bx+2ay=0$
On further simplification, we get
$\Rightarrow \left( a-b \right)\left( y-x \right)=0$
Thus, equation of the common chord is equal to
$\Rightarrow y-x=0$
We know that a line from the center of the circle perpendicularly bisects the chord.
Now, we will find the length of the perpendicular line from the center $\left( a,b \right)$ to the chord.
$\Rightarrow {{C}_{1}}M=\dfrac{\left| b-a \right|}{\sqrt{1+1}}$
On further simplification, we get
$\Rightarrow {{C}_{1}}M=\dfrac{b-a}{\sqrt{2}}$
Using Pythagoras theorem in $\vartriangle {{C}_{1}}MA$.
$\Rightarrow {{C}_{1}}{{A}^{2}}={{C}_{1}}{{M}^{2}}+M{{A}^{2}}$
Here ${{C}_{1}}A$ is the radius of the first circle and it is equal to $c$.
Substituting the value of length of all sides of a triangle, we get
$\Rightarrow {{c}^{2}}={{\left( \dfrac{b-a}{\sqrt{2}} \right)}^{2}}+M{{A}^{2}}$
On further simplification, we get
$\Rightarrow M{{A}^{2}}=\dfrac{2{{c}^{2}}-{{\left( b-a \right)}^{2}}}{2}$
Taking square root on both sides, we get
$\Rightarrow MA=\sqrt{\dfrac{2{{c}^{2}}-{{\left( b-a \right)}^{2}}}{2}}$
We know, the length of common chord $\left( AB \right)$ is equal to $2MA$ i.e.
$\Rightarrow AB=2MA$
Now, we will substitute the value of here.
$\Rightarrow AB=2\sqrt{\dfrac{2{{c}^{2}}-{{\left( b-a \right)}^{2}}}{2}}$
On simplifying the terms, we get
$\Rightarrow AB=\sqrt{4{{c}^{2}}-2{{\left( a-b \right)}^{2}}}$
Thus, the length of common chord is equal to $\sqrt{4{{c}^{2}}-2{{\left( b-a \right)}^{2}}}$.

Hence, the correct option is option C.

Note:
We need to know the meaning of following terms:-

1. A chord of a circle is defined as a line which is formed by joining two points lying on a circumference of a circle.
2. A common chord is formed between the two circles by joining the two intersecting points of these two circles.