Solveeit Logo
Login

Question

Question: The length of the common chord of two circles \( {\left( {x - a} \right)^2} + {\left( {y - b} \right...

The length of the common chord of two circles (x−a)2+(y−b)2=c2{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {c^2} and (x−b)2+(y−a)2=c2{\left( {x - b} \right)^2} + {\left( {y - a} \right)^2} = {c^2} is
(A) 4c2+2(a−b)2\sqrt {4{c^2} + 2{{\left( {a - b} \right)}^2}}
(B) 4c2+2(a+b)2\sqrt {4{c^2} + 2{{\left( {a + b} \right)}^2}}
(C) 4c2−2(a−b)2\sqrt {4{c^2} - 2{{\left( {a - b} \right)}^2}}
(D) c2−2(a−b)2\sqrt {{c^2} - 2{{\left( {a - b} \right)}^2}}

Explanation

Solution

Name the given circles as S1 and S2{S_1}{\text{ and }}{S_2} and use the equation S1−S2=0{S_1} - {S_2} = 0 to find the equation of the common chord. Now find the distance between the center of the circle and the chord using the formula for perpendicular distance between a point and a line, i.e. ∣Ax1+By1+C∣A2+B2\dfrac{{\left| {A{x_1} + B{y_1} + C} \right|}}{{\sqrt {{A^2} + {B^2}} }} . Now use the Pythagoras theorem to find the half-length of the chord.

Complete step by step solution:
Here in this problem, we are given two equations of a circle, which are (x−a)2+(y−b)2=c2{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {c^2} and (x−b)2+(y−a)2=c2{\left( {x - b} \right)^2} + {\left( {y - a} \right)^2} = {c^2} . And using the various properties of the circle and coordinate geometry we need to find the length of the common chord of these circles.
Two circles on the same plane can have one common point, two common points, or zero common points. We are here interested in the case where two circles are intersecting and have two common points and thus share a common chord.
Before starting with the solution, let us assume that circle S1≡(x−a)2+(y−b)2=c2{S_1} \equiv {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {c^2} and circle S2≡(x−b)2+(y−a)2=c2{S_2} \equiv {\left( {x - b} \right)^2} + {\left( {y - a} \right)^2} = {c^2} intersecting as two points ‘M’ and ‘N’, which makes the common chord of these circles. The centers of the circle S1 is C1{S_1}{\text{ is }}{C_1} and for S2 it is C2{S_2}{\text{ it is }}{C_2} .
Now using this information let’s make a diagram to visualize the situation better.

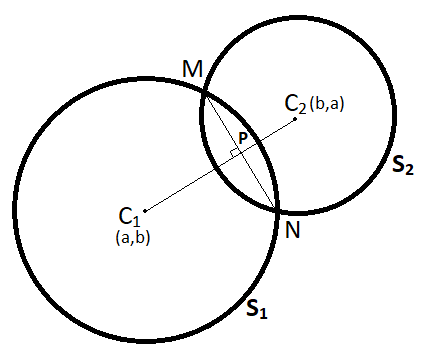
As we know from the coordinate geometry that the equation of a common chord for two circles S1 and S2{S_1}{\text{ and }}{S_2} can be given by: →S1−S2=0\to {S_1} - {S_2} = 0
On substituting the value of S1 and S2{S_1}{\text{ and }}{S_2} in the above equation of common chord, we get:
⇒((x−a)2+(y−b)2)−((x−b)2+(y−a)2)=c2−c2\Rightarrow \left( {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2}} \right) - \left( {{{\left( {x - b} \right)}^2} + {{\left( {y - a} \right)}^2}} \right) = {c^2} - {c^2}
This can be further solved using the algebraic identity (a−b)2=a2−2ab+b2{\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2} as:
⇒x2+a2−2xa+y2+b2−2yb−x2−b2+2xb−y2−a2+2ya=c2−c2=0\Rightarrow {x^2} + {a^2} - 2xa + {y^2} + {b^2} - 2yb - {x^2} - {b^2} + 2xb - {y^2} - {a^2} + 2ya = {c^2} - {c^2} = 0
Now we can subtract the same terms with opposite signs
⇒−2xa−2yb+2xb+2ya=0\Rightarrow - 2xa - 2yb + 2xb + 2ya = 0
Dividing the above equation by 22 , we get:
⇒−2xa−2yb+2xb+2ya2=0⇒xb+ya−xa−yb=0\Rightarrow \dfrac{{ - 2xa - 2yb + 2xb + 2ya}}{2} = 0 \Rightarrow xb + ya - xa - yb = 0
On factorizing and taking common, we can get a simplified form of the above equation:
⇒xb+ya−xa−yb=a(y−x)−b(y−x)=(a−b)(y−x)=0\Rightarrow xb + ya - xa - yb = a\left( {y - x} \right) - b\left( {y - x} \right) = \left( {a - b} \right)\left( {y - x} \right) = 0
Since ‘a’ and ‘b’ are considered to be not equal to each other. Therefore, we get the equation of the common chord as:
⇒x−y=0 or x=y\Rightarrow x - y = 0{\text{ or }}x = y
Thus, we get the equation of the MN as x=yx = y
The general form of the equation of a circle is given as (x−A)2+(y−B)2=C2{\left( {x - A} \right)^2} + {\left( {y - B} \right)^2} = {C^2} where the center of the circle will be at the point (A,B)\left( {A,B} \right) and the radius of the circle will be CC
Therefore, similarly for the given equations are (x−a)2+(y−b)2=c2{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {c^2} and (x−b)2+(y−a)2=c2{\left( {x - b} \right)^2} + {\left( {y - a} \right)^2} = {c^2} we got the center as C1(a,b) and C2(b,a){C_1}(a,b){\text{ and }}{C_2}(b,a) and both have radius ‘c’.
As we know that the perpendicular distance from a point (x1,y1)\left( {{x_1},{y_1}} \right) to a line Ax+By+C=0Ax + By + C = 0 is given by the expression =∣Ax1+By1+C∣A2+B2= \dfrac{{\left| {A{x_1} + B{y_1} + C} \right|}}{{\sqrt {{A^2} + {B^2}} }}
Similarly, the perpendicular distance C1P{C_1}P from a point C1(a,b){C_1}(a,b) to the line x=yx = y will be:
⇒C1P=∣a−b∣12+12=∣a−b∣2\Rightarrow {C_1}P = \dfrac{{\left| {a - b} \right|}}{{\sqrt {{1^2} + {1^2}} }} = \dfrac{{\left| {a - b} \right|}}{{\sqrt 2 }}
In the triangle ΔPMC1\Delta PM{C_1} , we can use Pythagoras theorem as:
⇒C1M2=C1P2+PM2\Rightarrow {C_1}{M^2} = {C_1}{P^2} + P{M^2}
Now we can find the measure of half of the common chord PM as:
⇒PM2=C1M2−C1P2⇒PM=C1M2−C1P2\Rightarrow P{M^2} = {C_1}{M^2} - {C_1}{P^2} \Rightarrow PM = \sqrt {{C_1}{M^2} - {C_1}{P^2}}
On substituting the known values in the above expression, we get:
⇒PM=C1M2−C1P2=c2−(∣a−b∣2)2=c2−(a−b)22\Rightarrow PM = \sqrt {{C_1}{M^2} - {C_1}{P^2}} = \sqrt {{c^2} - {{\left( {\dfrac{{\left| {a - b} \right|}}{{\sqrt 2 }}} \right)}^2}} = \sqrt {{c^2} - \dfrac{{{{\left( {a - b} \right)}^2}}}{2}}
Similarly, we can find the measure of PN which is equal to the PM
Therefore, PN=PM=c2−(a−b)22PN = PM = \sqrt {{c^2} - \dfrac{{{{\left( {a - b} \right)}^2}}}{2}}
The length of the common chord(MN) can be calculated by adding PN and PM together.
⇒MN=PN+PM=c2−(a−b)22+c2−(a−b)22=2c2−(a−b)22\Rightarrow MN = PN + PM = \sqrt {{c^2} - \dfrac{{{{\left( {a - b} \right)}^2}}}{2}} + \sqrt {{c^2} - \dfrac{{{{\left( {a - b} \right)}^2}}}{2}} = 2\sqrt {{c^2} - \dfrac{{{{\left( {a - b} \right)}^2}}}{2}}
Now we can simplify the expression by sending the 22 inside the radical sign:
⇒MN=2c2−(a−b)22=4c2−4×(a−b)22=4c2−2(a−b)2\Rightarrow MN = 2\sqrt {{c^2} - \dfrac{{{{\left( {a - b} \right)}^2}}}{2}} = \sqrt {4{c^2} - 4 \times \dfrac{{{{\left( {a - b} \right)}^2}}}{2}} = \sqrt {4{c^2} - 2{{\left( {a - b} \right)}^2}}
Thus we get the required length of the common chord as 4c2−2(a−b)2\sqrt {4{c^2} - 2{{\left( {a - b} \right)}^2}}

Hence, the option (C) is the correct answer.

Note:
In coordinate geometry, the use of properties of lines and formulas always plays a crucial part in the solution. For calculating the half-length of the chord, we used the Pythagoras theorem, which states that in any right triangle, the square of the length of the hypotenuse equals the sum of the squares of the lengths of the legs of the right triangle. Go step by step to avoid complications.