Question

The length of the common chord of the two circles

$${x^2} + {y^2} - 4y = 0{\text{ and }}{x^2} + {y^2} - 8x - 4y + 11 = 0 \\\ {\text{A}}{\text{. }}\sqrt {\dfrac{{145}}{4}} \\\ {\text{B}}{\text{. }}\sqrt {11} \\\ {\text{C}}{\text{. }}\sqrt {135} \\\ {\text{D}}{\text{. }}\sqrt {\dfrac{{135}}{4}} \\\$$

Answer 1

Hint-This question can be solved by Heron’s formula.

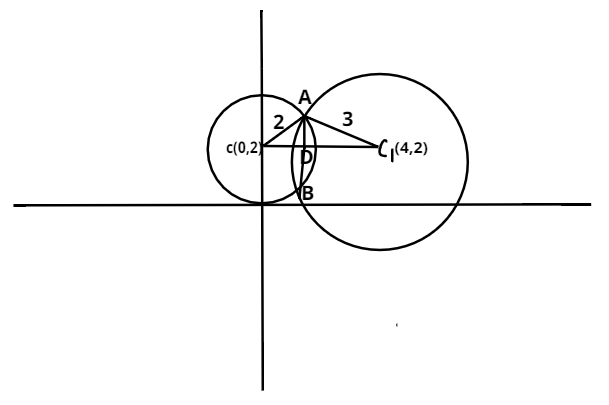
Now the given equations of the circles forming the common chord are
${x^2} + {y^2} - 4y = 0{\text{ and }}{x^2} + {y^2} - 8x - 4y + 11 = 0$ respectively
For better analysis of the problem let us draw the circles in the coordinate axis such that$\left( c \right)$
And $\left( {{c_1}} \right)$ be the center of the first and second circle respectively.
Now let$\left( A \right)$ and$\left( B \right)$ be the point of intersection of two circles.
Equation of first circle,${x^2} + {y^2} - 4y = 0$
Representing it in general form we get,
${x^2} + {\left( {y - 2} \right)^2} = 4$
Centre of this circle$\left( c \right) = \left( {0,2} \right)$
Similarly, Equation of second circle,${x^2} + {y^2} - 8x - 4y + 11 = 0$
Representing it in general form we get,
${\left( {x - 4} \right)^2} + {\left( {y - 2} \right)^2} = 9$
Centre of this circle$\left( {{c_1}} \right) = \left( {4,2} \right)$
Now to determine length of common chord, let us join$Ac$ ,$A{c_1}$ and$c{c_1}$ also$\left( {c{c_1} = 4} \right)$
$(Ac) = 2$ (i.e. radius of first circle) and$\left( {A{c_2}} \right) = 3$(i.e. radius of second circle)
Now the common chord is$\left( {AB} \right)$ so join$\left( {AB} \right)$.
Now draw a perpendicular from$A$ which intersects$c{c_1}$ at$D$ .
Now we know that by Heron’s formula, area of triangle${\text{ = }}\sqrt {S\left( {S - a} \right)\left( {S - b} \right)\left( {S - c} \right)}$
where$S = \dfrac{{a + b + c}}{2}$ and$\left( {a,b,c} \right)$ are lengths of sides of the triangle.
Using this formula we get$S = \dfrac{{2 + 3 + 4}}{2}$ where$\left( {a = 2,b = 3,c = 4} \right)$
Now area of triangle$Ac{c_1}$ $= \sqrt {\dfrac{9}{2}\left( {\dfrac{9}{2} - 2} \right)\left( {\dfrac{9}{2} - 3} \right)\left( {\dfrac{9}{2} - 4} \right)}$
$= \sqrt {\dfrac{9}{2} \times \dfrac{5}{2} \times \dfrac{3}{2} \times \dfrac{1}{2}} \\\ = \sqrt {\dfrac{{135}}{4}} \\\$
Similarly, we know that the area of triangle${\text{ = }}\dfrac{1}{2} \times perpendicular \times base$
From this we can calculate the value of$AD$and after that we will get the value of the common chord.

Area of triangle${\text{ = }}\dfrac{1}{2} \times AD \times c{c_1}$
$\sqrt {\dfrac{{135}}{4}} = \dfrac{1}{2} \times AD \times 4{\text{ }} \\\ \sqrt {\dfrac{{135}}{4}} \times \dfrac{2}{4} = AD \\\$ ($\because$ distance between$c{c_1} = 4$)
or$AD = \dfrac{1}{2}\sqrt {\dfrac{{135}}{4}}$
Now the length of common chord
${\text{ = 2}}AD = 2 \times \dfrac{1}{2}\sqrt {\dfrac{{135}}{4}} \\\ = \sqrt {\dfrac{{135}}{4}} \\\$
Thus the length of common chord${\text{ = }}\sqrt {\dfrac{{135}}{4}}$
The correct answer is$\left( D \right)$ .
Note-Whenever we face such types of problems the key concept is that we should draw the figure and
analyze the question like we did in this question. Here in this question we simply draw the two circles in
the coordinate axis to have a better analysis and then we find the area of the triangle by Heron’s
formula then we use this value to find the value of$AD$ then we find the value of the common chord.