Question
Question: The length of the common chord of the circle \({{\text{x}}^{\text{2}}}{\text{ + }}{{\text{y}}^{\text...
The length of the common chord of the circle x2 + y2+6x=0 and x2 + y2+3y=0 is
A. 56
B. 106
C. 106
D. 53
Solution
Hint: To solve this question we use the basic theory related to the topic common chord between two circles. As we know if we have two circles x2 + y2+6x=0 andx2 + y2+3y=0. then equation of common chord of the circles can be written as S1- S2=0. And then after using geometry we simply calculate the length of the common chord of the circle.
Complete step-by-step answer:
Let, S1: x2 + y2+6x=0
S2: x2 + y2+3y=0
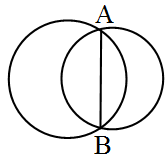
As we know,
Equation of common chord is: -
S1- S2=0
⇒ x2 + y2+6x-(x2 + y2+3y)=0
⇒ 6x-3y=0
⇒ 2x=y
⇒ 2x-y=0
Now, we have an equation of the common chord of given circles.
Perpendicular distance of 2x-y= 0 from (-3, 0).
Now, for simplification, we consider a single circle with a common chord of length AC.
Let, the first circle having radius OA and common chord is AC.
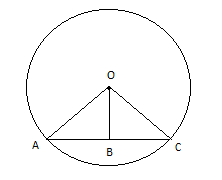
Here, OB=4+12×(−3)−0=5−6
And OA=r=3 (given)
Now use Pythagoras for AB.
AB=OA2 - OB2
= 32 - (5−6)2
= 9−536
= 545−36
= 53
Thus, The length of the common chord of the circle x2 + y2+6x=0 and x2 + y2+3y=0 is53.
Therefore, option (D) is the correct answer.
Note- In this question we have to used Pythagoras theorem which states that, in a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides (i.e. base and height of the given right-angled triangle) “.
