Question

The length of the chord $4y = 3x + 8$ of the parabola ${y^2} = 8x$ is:
A.$\dfrac{{320}}{7}$
B.$\dfrac{{320}}{9}$
C.$\dfrac{{80}}{9}$
D.$\dfrac{{640}}{7}$

Answer 1

First we have to find the point of intersection of the given chord and the curve using the method of substitution. It will give us two points of intersections, which are the endpoints of the chord. Then use the formula for the distance between two points in the$xy -$ plane to find the length of the chord using the obtained end points of the chord.

Complete step-by-step answer:
We have given the equation of the chord $4y = 3x + 8$ of the parabola${y^2} = 8x$. We have to find the length of the chord.

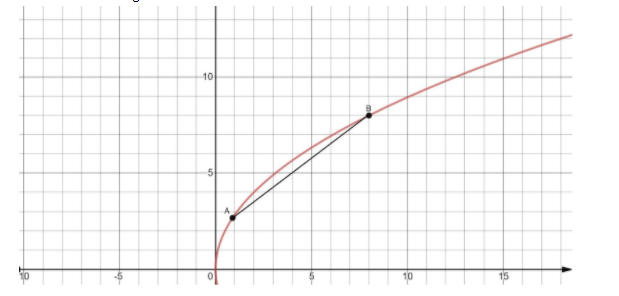
Consider the given equation of chord:
$4y = 3x + 8$
Now, we solve the equation for$x$:
$4y - 8 = 3x$
$x = \dfrac{{4y - 8}}{3}$ … (1)
Consider the given equation of the parabola:
${y^2} = 8x$
Now, we substitute $x = \dfrac{{4y - 8}}{3}$ into the above equation:
$\Rightarrow$ ${y^2} = 8\left( {\dfrac{{4y - 8}}{3}} \right)$
$\Rightarrow$ $3{y^2} = 32y - 64$
$\Rightarrow$ $3{y^2} - 32y + 64 = 0$
Factorize the expression by splitting the middle term.
$3{y^2} - 24y - 8y + 64 = 0$
$\Rightarrow$ $3y\left( {y - 8} \right) - 8\left( {y - 8} \right) = 0$
$\Rightarrow$ $\left( {y - 8} \right)\left( {3y - 8} \right) = 0$
Then, the obtained values of $y$are:
$\Rightarrow$ $y = 8{\rm{ or }} y = \dfrac{8}{3}$
Now, we substitute the value of $y$ into the equation (1) and evaluate the corresponding values of$x$.
$x = \dfrac{{4\left( 8 \right) - 8}}{3}$
$\Rightarrow$ $x = \dfrac{{24}}{3}$
$\Rightarrow$ $x = 8$
Similarly, $x = \dfrac{{4\left( {\dfrac{8}{3}} \right) - 8}}{3}$
$x = \dfrac{{\dfrac{{32}}{3} - 8}}{3}$
$\Rightarrow$ $x = \dfrac{{32 - 24}}{9}$
$\Rightarrow$ $x = \dfrac{8}{9}$
The obtained coordinates are $\left( {8,8} \right)$ and $\left( {\dfrac{8}{9},\dfrac{8}{3}} \right)$.
These coordinates are the end point of the chord. Now, we use the formula of distance between two points to find the length of the chord.
Assume $\left( {{x_1},{y_1}} \right) = \left( {8,8} \right)$ and $\left( {{x_2},{y_2}} \right) = \left( {\dfrac{8}{9},\dfrac{8}{3}} \right)$ , then we know that the distance between the points $\left( {{x_1},{y_1}} \right)$and$\left( {{x_2},{y_2}} \right)$is given as:
$L = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
Substitute $\left( {{x_1},{y_1}} \right) = \left( {8,8} \right)$ and $\left( {{x_2},{y_2}} \right) = \left( {\dfrac{8}{9},\dfrac{8}{3}} \right)$ into the above formula:
$\Rightarrow$ $L = \sqrt {{{\left( {\dfrac{8}{9} - 8} \right)}^2} + {{\left( {\dfrac{8}{3} - 8} \right)}^2}}$
Evaluate the chord length:
$L = \sqrt {{{\left( { - \dfrac{{64}}{9}} \right)}^2} + {{\left( { - \dfrac{{16}}{3}} \right)}^2}}$
$\Rightarrow$ $L = \sqrt {\dfrac{{4069}}{{81}} - \dfrac{{256}}{9}}$
$\Rightarrow$ $L = \sqrt {\dfrac{{4096 + 2304}}{{81}}}$
$\Rightarrow$ $L = \sqrt {\dfrac{{6400}}{{81}}}$
$\Rightarrow$ $L = \dfrac{{80}}{9}$
Therefore, the length of the chord is $\dfrac{{80}}{9}$ units.
Hence, the option (c) is the correct option.

Note: In the given equations, one equation is the linear equation and other one is the quadratic equation. It is easy to use the substitution method for solving the equations. If we use elimination methods then it becomes complex to find the solution.