Question

The length of shadow of a tree is 16 m when the angle of elevation of the sun is 60$^ \circ$. What is the height of the tree?
A.8 m
B.16 m
C.16$\sqrt 3$ m
D.$\dfrac{{{\text{16}}}}{{\sqrt {\text{3}} }}{\text{ m}}$

Answer 1

Hint: The Angle of elevation is the angle formed from the ground to the Top point of the object. Using the trigonometric value of that angle, we can use it to find the height of the object in this condition, where we have the length of the shadow.

Complete step-by-step answer:
Let’s begin with the given information of having the shadow length 16 m which is the distance between the tree bottom to the tip of the shadow. Another information is that the angle of elevation is 60$^ \circ$ which is inclined between the ground and the line between top of tree to ground.

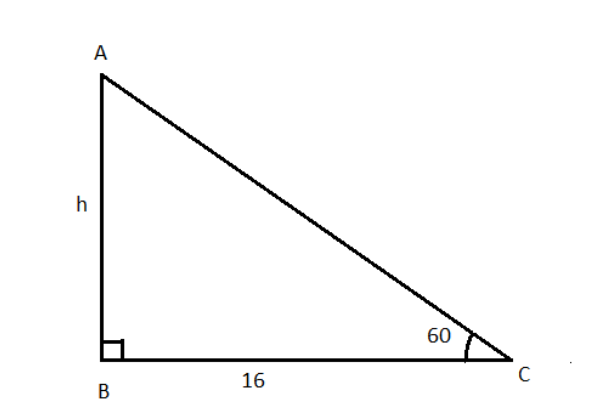
According to the figure, we get that

$$\tan {60^ \circ }\, = \,\dfrac{h}{{16}} \\\ h = \,16\,\tan {60^ \circ } \\\ = \,16\,\sqrt 3 \\\$$

Thus, the height of the tree is $16 \sqrt 3$ m.
Option c is the correct option.

Note: Angle of elevation is the angle formed by real line to the ground and angle of depression is angle formed while looking diagonally down to the horizon of the sky. Don’t confuse between the angle of elevation and angle of Deviation.