Question

The length of perpendicular from the point $(a\cos \alpha ,a\sin \alpha )$upon the straight line $y = x\tan \alpha + C,c > 0$is.
A. $a\cos \alpha$
B. $c{\sin ^2}x$
C. $c{\sec ^2}x$
D. $c{\cos ^2}x$

Answer 1

Perpendicular distance say (d) from a given point $P({x_1},{y_1})$to a line $Ax + By + c = 0$ is given as:
$\Rightarrow \dfrac{{|A{x_1} + B{y_1} + C|}}{{\sqrt {{A^2} + {B^2}} }}$. Use this formula to get the answer.

__
Complete step-by-step answer:
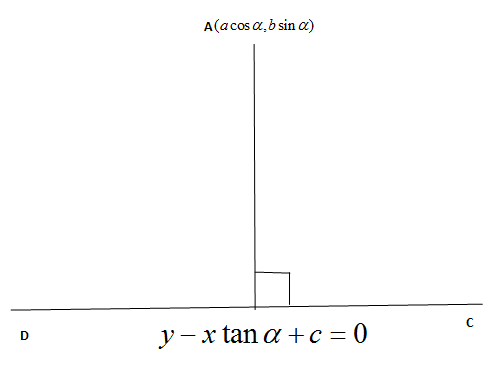
The given point is P$(a\cos \alpha ,a\sin \alpha )$.
And our equation of line is$y = x\tan \alpha + C$.
Perpendicular distance say (d) from a given point$P({x_1},{y_1})$to a line $Ax + By + c = 0$ is given as:
$\Rightarrow \dfrac{{|A{x_1} + B{y_1} + C|}}{{\sqrt {{A^2} + {B^2}} }}$.

$$\Rightarrow d = \dfrac{{|\left( { - \tan \alpha } \right)(a\cos \alpha ) + (1)(a\sin \alpha ) + c|}}{{\sqrt {{{\left( { - \tan \alpha } \right)}^2} + {{(1)}^2}} }} \\\ \Rightarrow d = \dfrac{{|\left( { - \dfrac{{\sin \alpha }}{{\cos \alpha }}} \right)(a\cos \alpha ) + (a\sin \alpha ) + c|}}{{\sqrt {1 + {{\tan }^2}\alpha } }} \\\ \Rightarrow d = \dfrac{{|( - a\sin \alpha ) + (a\sin \alpha ) + c|}}{{\sqrt {{{\sec }^2}\alpha } }} \\\ \Rightarrow d = \dfrac{c}{{\sec \alpha }} \\\ \Rightarrow d = c\cos \alpha \\\$$

None of the above options is correct.
The required perpendicular distance=$c\cos \alpha$.

Note: Working formula to solve such questions:
First simplify the equation of straight line.
Then put the points in our given straight line.
Then put the values in $\dfrac{{|A{x_1} + B{y_1} + C|}}{{\sqrt {{A^2} + {B^2}} }}$
Where, $Ax + By + C = 0$ is the equation of straight line and $({x_1},{y_1})$ are the points from which perpendicular distance is to be found.