Question

The length of perpendicular from $(3,1)$ on line $4x+3y+20=0$, is

1. 6
2. 7
3. 5
4. 8

Answer 1

In order to solve this problem, equation is given in the form of general equation of line that is $Ax+By+C=0$ then we will use distance formula which is $\dfrac{\left| A{{x}_{1}}+B{{y}_{1}}+{{C}_{1}} \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}$. Then compare the given equation with the standard equation, substitute in the distance formula and simplify the equations carefully.

Complete step-by-step solution:
We have given the equation of the line we have to find the perpendicular distance (d) of a line $4x+3y+20=0$ from a point C $(3,1)$. For better understanding figure is given below:

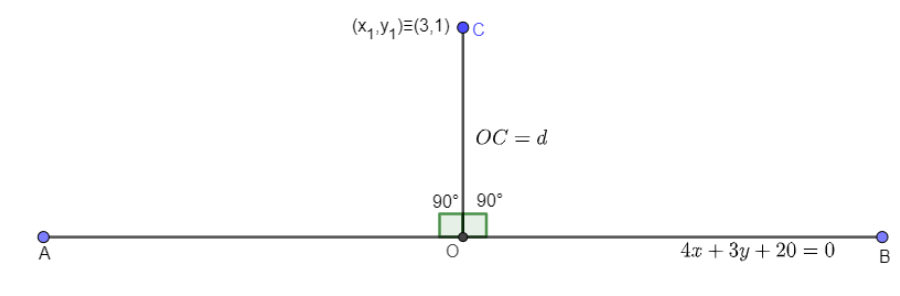
In the above figure, it is given that the length of perpendicular from the point C $(3,1)$ and consider the equation of line AB is given by
$\Rightarrow 4x+3y+20=0---(1)$
We know the general equation of line:
$\Rightarrow Ax+By+C=0---(2)$
By comparing the above equation (1) and (2) we get:
$\Rightarrow A=4$
$\Rightarrow B=3$
$\Rightarrow C=20$
Consider the points as $({{x}_{1}},{{y}_{1}})$ in the given figure and according to the question it is given by ${{x}_{1}}=3$ and ${{y}_{1}}=1$
Length of perpendicular distance from above figure is $OC=d$
Distance formula is given by
$\Rightarrow d=\dfrac{\left| A{{x}_{1}}+B{{y}_{1}}+C \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}$
Place the value of ${{x}_{1}}$, ${{y}_{1}}$, $A$, $B$ and $C$ we get:
$\Rightarrow d=\dfrac{\left| \left( 4\times 3 \right)+\left( 3\times 1 \right)+20 \right|}{\sqrt{{{4}^{2}}+{{3}^{2}}}}$
By simplifying further, we get:
$\Rightarrow d=\dfrac{\left| 12+3+20 \right|}{\sqrt{16+9}}$
By further solving this equation we get:
$\Rightarrow d=\dfrac{\left| 35 \right|}{\sqrt{25}}$
As we know that $\sqrt{25}=5$ and $\left| 35 \right|=35$ substitute these values on above equation we get:
$\Rightarrow d=\dfrac{35}{5}$
By reducing this fraction, we get:
$\Rightarrow d=7$
Hence, perpendicular distance $OC=d=7$
So, the correct option is “option 2”.

Note: Remember all of the trigonometric formulas and how they are related. The most crucial step is to make the correct substitution. Simplification should be done with care, taking into account all of the given points as well as the line equation. We can also see that there is a modulus sign in the numerator, indicating that we should always consider the positive sign. As a result, we must determine the distance; distance is always positive. We are also assuming that the distance we are measuring is the shortest distance between the point and the line, which is the perpendicular distance.