Question

The length of latus rectum of$xy = 4$ is

Answer 1

Start by writing the standard equation of rectangular hyperbola, which can be obtained by rotating the hyperbola by ${45^ \circ }$ clockwise, and find out the length of the latus rectum by comparing the terms with standard equations.

Complete step by step answer:

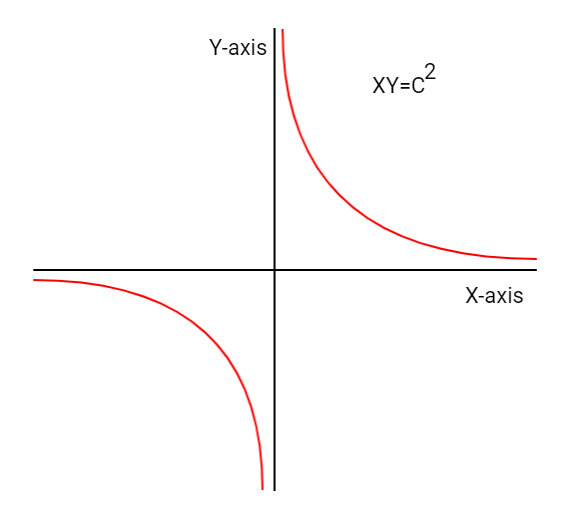
Given, $xy = 4$
We know that, equation of rectangular hyperbola = $xy = \dfrac{{{a^2}}}{2}$
And we also know , Length of latus rectum for hyperbola ${x^2} - {y^2} = {a^2}$ is given by the relation$\dfrac{{2{b^2}}}{a}$ where ‘b’ is the minor axis and ‘a’ is major axis $= \dfrac{{2{a^2}}}{a} = 2a$
Therefore, length of latus rectum of hyperbola is 2a
Now, if we rotate the hyperbola by ${45^ \circ }$ in clockwise direction, ${x^2} - {y^2} = {a^2}$will become $xy = {c^2}\left( {{\text{here }}{c^2} = \dfrac{{{a^2}}}{2}} \right)$
It is already given that $xy = 4$
On comparison with the $xy = {c^2}$, we get
${c^2} = 4 \\\ \Rightarrow \dfrac{{{a^2}}}{2} = 4 \\\ \Rightarrow {a^2} = 8 \\\ \Rightarrow a = 2\sqrt 2 \\\$

Length of the latus rectum $= 2a = 2 \times 2\sqrt 2$ which can also be written as $4\sqrt 2$.

Note: In order to solve this question one must know the concept of latus rectum that is a latus rectum of a conic section is the chord through a focus parallel to the conic section directrix. By using this approach one can easily find the solution.