Solveeit Logo
Login

Question

Question: The length of intercept cut off from the line y = mx +c by the circle \({{\text{x}}^2} + {{\text{y}}...

The length of intercept cut off from the line y = mx +c by the circle x2+y2=a2{{\text{x}}^2} + {{\text{y}}^2} = {a^2} is
A.a2(1+m2)−c2\sqrt {{{\text{a}}^2}\left( {1 + {m^2}} \right) - {c^2}}
B. a2(1+m2)−c21+m2\dfrac{{\sqrt {{{\text{a}}^2}\left( {1 + {m^2}} \right) - {c^2}} }}{{\sqrt {1 + {m^2}} }}
C. 2a2(1+m2)−c21+m2\dfrac{{2\sqrt {{{\text{a}}^2}\left( {1 + {m^2}} \right) - {c^2}} }}{{\sqrt {1 + {m^2}} }}
D. a2(1+m2)−c2{{\text{a}}^2}\left( {1 + {m^2}} \right) - {c^2}

Explanation

Solution

Hint: In this question, first we will make the diagram with the centre of the circle as (0,0) and radius as ‘a’. After this we will draw a perpendicular from centre to chord form by the given line. Then determine the length of the perpendicular and use it to calculate the length of chord.

Complete step-by-step answer:
The diagram for the question is:

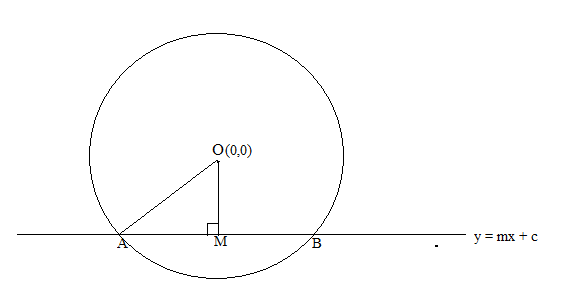
OM is the perpendicular drawn from centre o. It divides AB into two parts such that AM = BM.
OA is the radius = a

We know that length of perpendicular drawn from point(x1,y1{{\text{x}}_1},{{\text{y}}_1}) is given by:
d = |ax1+by1+c∣a2+b2\dfrac{{{\text{|a}}{{\text{x}}_1} + {\text{b}}{{\text{y}}_1} + c|}}{{\sqrt {{{\text{a}}^2} + {{\text{b}}^2}} }}
Therefore, we can say that:
OM = c1+m2\dfrac{c}{{\sqrt {1 + {m^2}} }}
Using Pythagoras theorem, we can write:
AM2=OA2−OM2{\text{A}}{{\text{M}}^2} = {\text{O}}{{\text{A}}^2} - {\text{O}}{{\text{M}}^2}
Putting the values in above equation, we get:
AM2=a2−(c1+m2)2{\text{A}}{{\text{M}}^2} = {{\text{a}}^2} - {\left( {\dfrac{c}{{\sqrt {1 + {m^2}} }}} \right)^2}
⇒\Rightarrow AM=a2−(c1+m2)2=a2−c2(1+m2)=a2(1+m2)−c2(1+m2){\text{AM}} = \sqrt {{{\text{a}}^2} - {{\left( {\dfrac{c}{{\sqrt {1 + {m^2}} }}} \right)}^2}} = \sqrt {{{\text{a}}^2} - \dfrac{{{c^2}}}{{{{(1 + {m^2})}^{}}}}} = \sqrt {\dfrac{{{{\text{a}}^2}(1 + {m^2}) - {c^2}}}{{{{(1 + {m^2})}^{}}}}}
Therefore, length chord AB = 2a2(1+m2)−c2(1+m2)2\sqrt {\dfrac{{{{\text{a}}^2}(1 + {m^2}) - {c^2}}}{{{{(1 + {m^2})}^{}}}}}
So, option C is correct.

Note- In the question involving finding the length of the chord, you should remember the formula for finding the length of perpendicular drawn from a point(x1,y1{{\text{x}}_1},{{\text{y}}_1}) which is given by:
d = |ax1+by1+c∣a2+b2\dfrac{{{\text{|a}}{{\text{x}}_1} + {\text{b}}{{\text{y}}_1} + c|}}{{\sqrt {{{\text{a}}^2} + {{\text{b}}^2}} }} . You should know that the perpendicular drawn from centre on the chord divides the chord into two equal parts.