Question

The length of double ordinate of parabola ${{y}^{2}}=8x$ which subtends an angle ${{60}^{\circ }}$ at vertex in
(a) $4\sqrt{3}$
(b) $8\sqrt{3}$
(c) $16\sqrt{3}$
(d) $324\sqrt{3}$

Answer 1

Hint: Draw figure of parabola ${{y}^{2}}=8x$. Consider the point on parabola as$(a{{t}^{2}},2at)$. Thus first the value of a and t, thus from the points of parabola and find the length of double ordinate.

Complete step-by-step answer:
We have been given the equation of parabola as${{y}^{2}}=8x$. We know that the general representation of a parabola is${{y}^{2}}=4ax$. Where 4a is latus rectum. By comparing both general equation and the given equation of parabola, we can say that
$4a=8$
$\therefore \,\,\,a=\dfrac{8}{4}=2$
We know that the point of parabola is $(a{{t}^{2}},2at)$, put $a=2$. Thus we can make out the ordinate of parabola as $(2{{t}^{2}},4t)$. Let this be point P.
Thus the end points of double ordinate of parabola ${{y}^{2}}=8x$ are P$(2{{t}^{2}},4t)$ and $P'(2{{t}^{2}},-4t)$.
Check the figure.

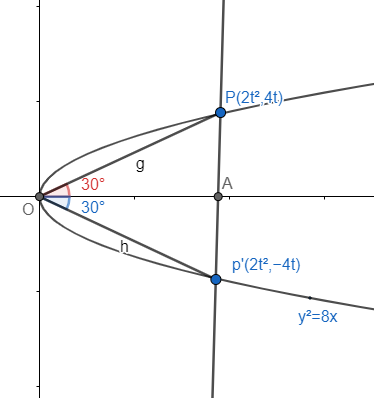
It is given that the double ordinate is subtended at an angle ${{60}^{\circ }}$.
This angle ${{60}^{\circ }}$is bisected by the axis of the parabola.
Thus taking $\tan {{30}^{\circ }}$we get
$\tan {{30}^{\circ }}=\dfrac{\text{Opposite side}}{\text{adjacent side}}=\dfrac{\text{AP}}{\text{OA}}$
$\tan {{30}^{\circ }}=\dfrac{\text{4t}}{\text{2}{{\text{t}}^{\text{2}}}}$
From trigonometric table, we know that
$\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}$
$\therefore \dfrac{1}{\sqrt{3}}=\dfrac{\text{2}}{\text{t}}\Rightarrow \text{t}=2\sqrt{3}$
$\therefore$Point P$(2{{t}^{2}},4t)$becomes

& P(2\times {{(2\sqrt{3})}^{2}},4\times 2\sqrt{3} \\\ & =P(24,8\sqrt{3}) \\\ \end{aligned}$$ Similarly point $$P'(2{{t}^{2}},-4t)$$becomes $$P'(24,8\sqrt{3})$$ $$\therefore $$ We got the point as $$P(24,8\sqrt{3})$$and $$P'(24,8\sqrt{3})$$. What we need is the length of the double ordinate, we need to find PP’. We can find it using the distance formula, $$\begin{aligned} & \sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}=\text{distance formula} \\\ & ({{x}_{1}},{{y}_{1}})=(24,8\sqrt{3)} \\\ & ({{x}_{2}},{{y}_{2}})=(24,-8\sqrt{3)} \\\ \end{aligned}$$ $$\therefore \text{length of PP }\\!\\!'\\!\\!\text{ = }\sqrt{(24-24)+{{\left[ \left( 8\sqrt{3} \right)-\left( -8\sqrt{3} \right) \right]}^{2}}}$$ $$\begin{aligned} & =\sqrt{0+{{\left( 8\sqrt{3}+8\sqrt{3} \right)}^{2}}} \\\ & =\sqrt{{{\left( 16\sqrt{3} \right)}^{2}}} \\\ & =16\sqrt{3} \\\ \end{aligned}$$ Thus we got the length of the double ordinate as $$16\sqrt{3}$$. $$\therefore $$Option (c) is the correct answer. Note: The double ordinate of parabola is any chord which is perpendicular to the axis of parabola. Here PA and P’A are the two chords which are perpendicular to the axis of the parabola, that’s why it is called a double ordinate.