Question

The length of common tangent to the circle of radii $12$cm and $4$cm is $15$ cm. The distance between their centers is $17$cm.
A) True B) False

Answer 1

We can solve the problem by using pythagoras theorem by making figure on given conditions or we can also solve using the formula ${\text{d = }}\sqrt {{{\text{t}}^2} + {{\left( {{{\text{r}}_1} - {{\text{r}}_2}} \right)}^2}}$ where d is the distance between the centers of two circles with radii ${{\text{r}}_1}$ and ${{\text{r}}_2}$, and t is the length of the common tangent. On putting the given values, you’ll get the answer.

Complete step by step answer:

Given, the length of common tangent to the circles = $15$cm and the radii of the two circles are $12$cm and $4$cm. We have to find the distance between their centers. Let A and B be the centers of the two circles respectively and CD be the common tangent to the circles. Let us draw EB $\parallel$CD to make rectangle BDCE where CD=EB=$15$cm and EC=BD= $4$cm

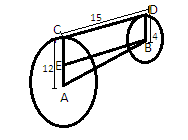
Now from the figure, AE=AC-CE
$\Rightarrow {\text{AE = 12 - 4 = 8}}$ cm

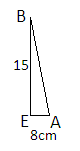
Now In the triangle BEA, We know EB and AE but we have to find AB.
Let AB=x cm. Since ∆ BEA is a right-angled triangle, we can use the Pythagoras theorem to find AB. According to the Pythagoras theorem, “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides.”It can be written as-
$\Rightarrow$ ${{\text{H}}^2} = {{\text{P}}^2}{\text{ + }}{{\text{B}}^2}$
Where H is the hypotenuse, P is the perpendicular and B is the base of the triangle.
In triangle BEA, H=AB, P=EB and B=AE
Then on using the formula, we get
$\Rightarrow$ ${\left( {{\text{AE}}} \right)^2} + {\left( {{\text{EB}}} \right)^2} = {\text{A}}{{\text{B}}^2}$
$\Rightarrow {{\text{x}}^2} = {\left( 8 \right)^2} + {\left( {15} \right)^2} = 64 + 225 = 289 \\\ \Rightarrow {\text{x}} = \sqrt {289} = 17 \\\$
AB=$17$ cm= the distance between the centers of the two circles. So the statement is true.
Hence the correct answer is ‘A’.
Note: : We can also use the formula ${\text{d = }}\sqrt {{{\text{t}}^2} + {{\left( {{{\text{r}}_1} - {{\text{r}}_2}} \right)}^2}}$ where d is the distance between the centers of two circles with radii ${{\text{r}}_1}$ and${{\text{r}}_2}$, and t is the length of the common tangent and we’ll get the same answer. This formula is used when the circles have a direct common tangent. On putting the given values we get,
$\Rightarrow$ d=$\sqrt {{{15}^2} + {{\left( {12 - 4} \right)}^2}} = \sqrt {225 + {8^2}} = \sqrt {225 + 64}$
$\Rightarrow$ d=$\sqrt {289} = 17$ cm
But If the circles have transverse common tangent (see the figure)-

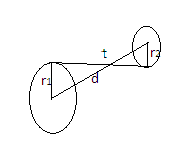
Then we use formula for distance between their centers ${\text{d = }}\sqrt {{{\text{t}}^2} + {{\left( {{{\text{r}}_1}{\text{ + }}{{\text{r}}_2}} \right)}^2}}$ where the notations have same meaning.