Question

The length of a wire of cross-sectional area $1\times {{10}^{-6}}{{m}^{2}}$ is 10m. The young’s modulus of the material of the wire is 25 G.pa. When the wire is subjected to a tensile force of 100N, the elongation produced in mm is:
A. 0.04
B. 0.4
C. 4
D. 40

Answer 1

As we know, Young’s modulus is the ratio of longitudinal stress to the longitudinal strain. Just like any other stress, longitudinal stress (σ) is given by the force by area and longitudinal strain (ε) by the ratio of change in length to the body’s original length. Now, you could substitute these relations in place of σ and ε and then rearranging gives you the required change in length. Also,
$1GPa={{10}^{9}}N{{m}^{-2}}$ .

Formula used: $Y=\dfrac{F\times L}{A\times \Delta L}$

Complete step by step answer:
We know that Young's modulus is the ratio of tensile (or compressive) stress (σ) to the longitudinal strain (ε). It is normally represented by ‘Y’. Young’s modulus can be given by,
$Y=\dfrac{\sigma }{\varepsilon }$ …………………. (1)

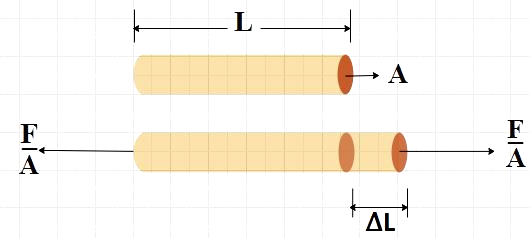
Let us understand what stress and strain really are.
Tensile stress or compressive stress is otherwise called longitudinal stress. In the case of longitudinal stress, the force applied is normal to its cross-sectional area and is represented by σ. If the body is stretched as the result of applying stress, then applied stress is tensile, instead, if the body is compressed, it is compressive stress. Longitudinal stress is given by,
$\sigma =\dfrac{F}{A}$ …………….. (2)
Longitudinal strain, represented by ε, is simply the ratio of change in length (∆L) to the original length (L) of the body on which the longitudinal stress is applied. That is,
$\varepsilon =\dfrac{\Delta L}{L}$ …………………… (3)
Therefore, substituting (2) and (3) in (1), we get Young’s modulus as,
$Y=\dfrac{\dfrac{F}{A}}{\dfrac{\Delta L}{L}}$
$Y=\dfrac{F\times L}{\begin{aligned} & A\times \Delta L \\\ & \\\ \end{aligned}}$
We are supposed to find change in length ∆L in the given question, so,
$\Delta L=\dfrac{F\times L}{A\times Y}$ ……………. (4)
Since all the values are given, we could directly substitute them in (4)
Since Y is given in units of Giga Pascal.
We have, $1GPa={{10}^{9}}N{{m}^{-2}}$
Therefore, $25GPa=25\times {{10}^{9}}N{{m}^{-2}}$
Equation (4) now becomes,
$\Delta L=\dfrac{100N\times 10m}{\left( 1\times {{10}^{-6}} \right){{m}^{2}}\times \left( 25\times {{10}^{9}} \right)N{{m}^{-2}}}$
$\Delta L=0.04m$
Since the options are given in millimeters, we have to convert this value.
$\Delta L=0.04m=40mm$

So, the correct answer is “Option D”.

Note: While dealing with numerical problems like this, we should convert all the given values into their respective SI units and then carry out the calculation so as to avoid further confusion. Also, make sure whether the options are given in their SI units, if not, convert accordingly. Note that, in this question the answer is asked in millimeters, so we have to convert the value in millimeter terms.