Question
Question: The length of a rod under longitudinal tension $T_1$ is $L_1$ and that under longitudinal tension $T...
The length of a rod under longitudinal tension T1 is L1 and that under longitudinal tension T2 is L2. What is the actual length of the rod, in the absence of tensions?
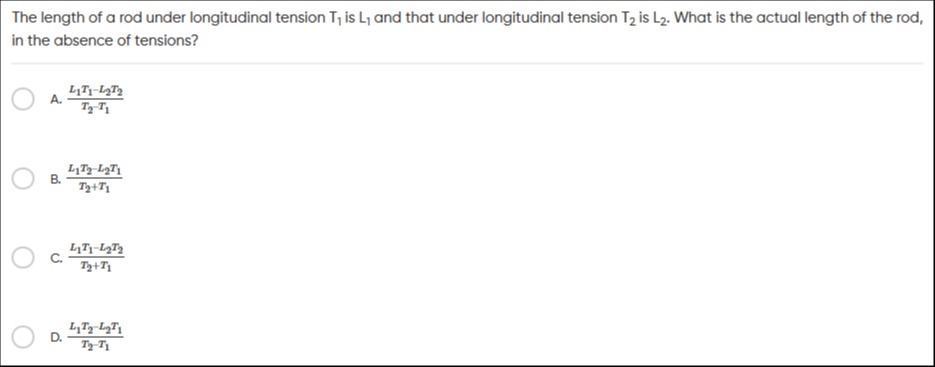
T2−T1L1T1−L2T2
T2+T1L1T2−L2T1
T2+T1L1T1−L2T2
T2−T1L1T2−L2T1
T2−T1L1T2−L2T1
Solution
The length of a rod under longitudinal tension T is given by L=L0(1+AYT), where L0 is the original length. This can be written as L=L0+(AYL0)T. This is a linear relationship between L and T. We have two points (T1,L1) and (T2,L2). The equation of the line passing through these points is T−T1L−L1=T2−T1L2−L1. The actual length of the rod in the absence of tension is L0, which is the value of L when T=0. Substituting T=0 and L=L0: 0−T1L0−L1=T2−T1L2−L1. Solving for L0: L0=L1−T1(T2−T1L2−L1)=T2−T1L1(T2−T1)−T1(L2−L1)=T2−T1L1T2−L1T1−T1L2+T1L1=T2−T1L1T2−L2T1.
