Question

The length of a potentiometer wire is l. A cell of emf E is balanced at a length $\dfrac{l}{5}$ from the positive end of the wire. If the length of the wire is increased by $\dfrac{l}{2}$, the distance of the balance point with the same cell is
A. $\dfrac{2}{{15}}l$
B. $\dfrac{3}{{15}}l$
C. $\dfrac{3}{{10}}l$
D. $\dfrac{4}{{10}}l$

Answer 1

Calculate the potential gradient of the cell in the first case and then determine the emf of the cell using the relation between emf, potential gradient and distance of the position of the balance point. Then determine the potential gradient in the second case and determine the emf. Equate the two equations you obtained.

Formula used:
Potential gradient,
$K = \dfrac{E}{l}$
Here, E is the emf of the cell and l is the length of the potentiometer wire.
Emf of the cell at a particular position on the potentiometer wire is,
$\varepsilon = K\,{l_1}$
Here, ${l_1}$ is the length of the wire from the positive end

Complete step by step answer:
We have given that the emf is balanced at position $\dfrac{l}{5}$, from the positive end of the wire as shown in the figure below,

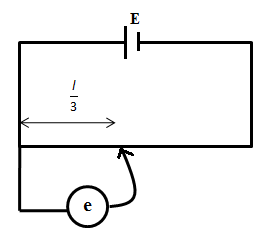
We can express the potential gradient of the wire as follows,
${K_1} = \dfrac{E}{l}$ …… (1)
Since we have given that the emf is balanced at position $\dfrac{l}{5}$ from the left of the wire as shown in the above figure, we can express the emf of the cell at this position as,
${\varepsilon _1} = {K_1}\dfrac{l}{5}$
Using equation (1) in the above equation, we get,
${\varepsilon _1} = \dfrac{E}{l}\dfrac{l}{5}$
$\Rightarrow {\varepsilon _1} = \dfrac{E}{5}$ …… (2)
Now, the length of the potentiometer wire is increased by $\dfrac{l}{2}$, the new length of the wire is,
${l_2} = l + \dfrac{l}{2}$
$\Rightarrow {l_2} = \dfrac{{3l}}{2}$
Therefore, we can see the potential gradient of the cell will change to,
${K_2} = \dfrac{E}{{{l_2}}}$
$\Rightarrow {K_2} = \dfrac{E}{{\dfrac{{3l}}{2}}}$
$\Rightarrow {K_2} = \dfrac{{2E}}{{3l}}$
We assume the balance point is at a distance x from the positive end. Therefore, we can express the emf of the cell at this position as follows,
${\varepsilon _2} = {K_2}x$
$\Rightarrow {\varepsilon _2} = \dfrac{{2E}}{{3l}}\,x$ …… (3)
We equate equation (2) and (3) as follows,
$\dfrac{E}{5} = \dfrac{{2E}}{{3l}}\,x$
$\Rightarrow x = \dfrac{{3l}}{{10}}$

Therefore, the balance point in the second case will be at $\dfrac{{3l}}{{10}}$.

So, the correct answer is “Option C”.

Note:
Note that the potential gradient K changes with the length of the potentiometer wire.
It should be the ratio of the emf of the cell to the total length of the wire and should not be the emf shown by the deflection per unit distance from the positive end.
The emf of the cell using the relation between emf, potential gradient and distance of the position of the balance point.