Question

The length of a potentiometer wire is $1200cm$ and it carries a current of $60mA$. For a cell of emf $5V$ and internal resistance of $20\Omega$, the null point on it is found to be at $1000cm$. The resistance of the whole wire is:
A. $60\Omega$
B. $100\Omega$
C. $80\Omega$
D. $120\Omega$

Answer 1

The potentiometer wire works on the principle – the potential drop across a given part of wire is directly proportional to the length of that part of the wire. The resistance of the potentiometer wire can be found by firstly finding the potential drop across the potentiometer. Using the potential drop across potentiometer wire, we can find the resistance using Ohm’s Law.

Formula used:
${R_{AB}} = \dfrac{{{V_{AC}}}}{I} \times \dfrac{{{L_{AB}}}}{{{L_{AC}}}}$

Complete answer:
First and foremost, we’ll draw a rough circuit diagram, for better understanding.

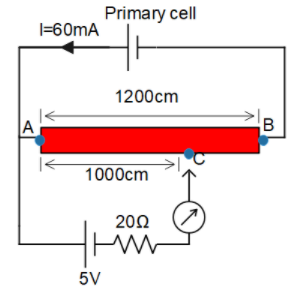
In the diagram,
$AB$ is the potentiometer wire
$C$ is the null point
$I$ is the current passing through the potentiometer wire.
From the diagram, we’ll first find the potential drop across, AB using the balancing length of potentiometer formula. It is given by
$\dfrac{{{V_{AB}}}}{{{L_{AB}}}} = \dfrac{{{V_{AC}}}}{{{L_{AC}}}}$
We have, ${L_{AB}} = {\text{ }}1200cm$, ${V_{AC}} = {\text{ }}5V$, ${L_{AC}} = {\text{ }}1000cm$. So, by solving for ${V_{AB}}$
\eqalign{ & \dfrac{{{V_{AB}}}}{{{L_{AB}}}} = \dfrac{{{V_{AC}}}}{{{L_{AC}}}} \Rightarrow {V_{AB}} = \dfrac{{{V_{AC}}}}{{{L_{AC}}}} \times {L_{AB}} \cr & \Rightarrow {V_{AB}} = \dfrac{{5V}}{{1000cm}} \times 1200cm \cr & \Rightarrow {V_{AB}} = 6V \cr}
Now, using Ohm’s Law, we can find the resistance of potentiometer wire. From ohm’s law we have
${V_{AB}} = I{R_{AB}} \Rightarrow {R_{AB}} = \dfrac{{{V_{AB}}}}{I}$
Here
${R_{AB}}$ is the resistance of potentiometer wire
$I$ is the current passing through the potentiometer wire
${V_{AB}}$ is the potential drop across the potentiometer wire
\eqalign{ & \Rightarrow {R_{AB}} = \dfrac{{6V}}{{60 \times {{10}^{ - 3}}A}} = 100\Omega \cr & \therefore {R_{AB}} = 100\Omega \cr}

Therefore, the correct option is B.

Note:
The principle of potentiometer wire is dependent on potential gradient. It is given by,
$K = \dfrac{{dV}}{{dx}}$ $B.{\text{ }}100\Omega$
Where
$K$ is the potential gradient
$V$ is voltage
$x$ is the length of displacement
differentiation with respect to x indicates the rate of change of voltage with respect to the length.
For a given wire of the same physical properties, the potential gradient is constant.