Question

The length of a focal chord of the parabola ${y^2} = 4ax$ at a distance $b$ from the vertex is $c$ , then
(A) $2{a^2} = bc$
(B) ${a^3} = {b^2}c$
(C) $ac = {b^2}$
(D) ${b^2}c = 4{a^3}$

Answer 1

Here, we need to find which of the given expressions is true. A focal chord is any chord that passes through the focus of a parabola. Here we have to suppose that the focal chord makes an angle of $\theta$ with the $x$ axis. Using the given lengths, we will find the sine of angle $\theta$. Then, we will substitute the value of $\sin \theta$ in the formula for length of a focal chord that makes an angle $\theta$ with the $x$ axis.
Formula Used: Here, we will use the formula of length of the focal cord, $c = 4a{\rm{cose}}{{\rm{c}}^2}\theta$, where $c$ is the length of focal cord and $a$ is the point on the plane.

Complete step by step solution:
First, we will draw the diagram for the given problem.

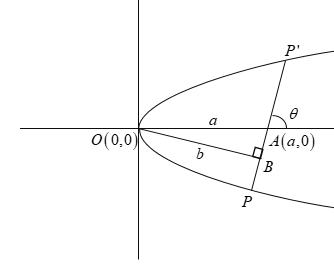
Here, the focus $A$ lies on the point $\left( {a,0} \right)$. The distance between the vertex and the focus is $OA = a$. The focal chord is $PP'$, which is of length $c$ and makes an angle $\theta$ with the $x$ axis. The perpendicular distance between the vertex and the focal chord is $OB = b$.
The length of a focal chord of a parabola is given by $4a{\rm{cose}}{{\rm{c}}^2}\theta$, where the focus of the parabola lies on the point $\left( {a,0} \right)$, and $\theta$ is the angle between the focal chord and the $x$ axis.
The length of the focal chord is $c$. Thus, we get
$c = 4a{\rm{cose}}{{\rm{c}}^2}\theta$………$\left( 1 \right)$
Now, we know that vertically opposite angles are equal.
Therefore, $\angle OAB = \theta$.
We will find the sine of the angle $\theta$ using the right triangle $OAB$.
In right triangle $OAB$, we have
$\begin{array}{l}\sin \theta = \dfrac{{{\rm{Perpendicular}}}}{{{\rm{Hypotenuse}}}}\\\ \Rightarrow \sin \theta = \dfrac{{OB}}{{OA}}\end{array}$
Substituting $OA = a$ and $OB = b$ in the expression, we get
$\Rightarrow \sin \theta = \dfrac{b}{a}$
Next, we know that the cosecant of an angle is the reciprocal of the sine of that angle.
Thus, we can find ${\rm{cosec}}\theta$ as
${\rm{cosec}}\theta = \dfrac{1}{{\sin \theta }}$
Substituting $\sin \theta = \dfrac{b}{a}$, we get
$\begin{array}{l}{\rm{cosec}}\theta = \dfrac{1}{{\dfrac{b}{a}}}\\\ = \dfrac{a}{b}\end{array}$
Substitute ${\rm{cosec}}\theta = \dfrac{a}{b}$ in equation $\left( 1 \right)$, we get the equation
$c = 4a{\left( {\dfrac{a}{b}} \right)^2}$
Simplifying the expression, we get
$\begin{array}{l} \Rightarrow c = 4a\left( {\dfrac{{{a^2}}}{{{b^2}}}} \right)\\\ \Rightarrow c = \dfrac{{4{a^3}}}{{{b^2}}}\\\ \Rightarrow {b^2}c = 4{a^3}\end{array}$

$\therefore$ The option (c) is correct.

Note:
Parabola is a curve in which the fixed point is called focus and directrix is a fixed straight line. Any point on the parabola is at equidistant from focus and the directrix. While solving this question we need to first understand the difference between focal chord and focal distance. A focal chord is any chord that passes through the focus of a parabola. While, the distance between a point and the focus is called focal distance of that point.