Question

The length of a compound microscope is $14\; cm$ and its magnifying power when the final image is formed at a near point is $2\;5$. If the focal length of the eyepiece is $5\;cm$. The distance of object form the objective and the focal length of objective lens are:
$A. \dfrac{59}{25}\;cm, \dfrac{69}{31}\;cm$
$B. \dfrac{59}{31}\;cm, \dfrac{69}{25}\;cm$
$C. 3\; cm, 2 \;cm$
$D. 4\;cm, 1\;cm$

Answer 1

Compound microscope is a system of lenses which produces enlarged images of the object. It follows lens law and magnification formula as given below. We use $D=25cm$ as the distance till which the relaxed eyes can see .
Formula used:
$\dfrac{1}{u_{o}}+\dfrac{1}{v_{o}}=\dfrac{1}{f_{o}}$
$m=\dfrac{v_{o}}{u_{o}}\left(\dfrac{D}{f_{e}}\right)$

Complete answer:
Given that,
Focal length of eyepiece=$f_{e}=5cm$,
Length of the microscope is $L=14 cm$,
Magnifying power=$m=25$
Let us consider the ray diagram as shown below:
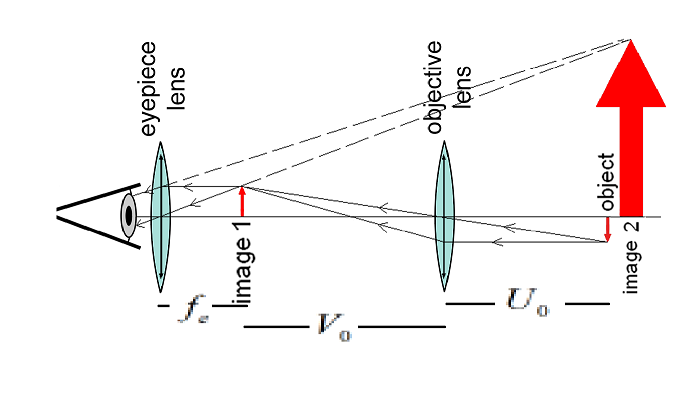Where $V_{O}$ is the distance of the image formed due to the objective lens and $U_{O}$ is the distance due to the object for the objective lens.
Clearly, from the figure we can say that $V_{O}+f_{e}=L$
$\implies V_{O}=L-f_{e}$
$\implies V_{O}=14-5=9\;cm$
We also know that magnifying power ,$m=\dfrac{v_{o}}{u_{o}}\left(\dfrac{D}{f_{e}}\right)$, where $D$ is the distance a relaxed eye can see.
Now rearranging, we get
$m=\dfrac{v_{o}}{u_{o}}\left(\dfrac{D}{f_{e}}\right)$,
Substituting, we get
$\implies U_{O}=\dfrac{9}{25}\times \dfrac{25}{5}$
$\therefore U_{O}=\dfrac{9}{5}=1.8\;cm$
Now to calculate the focal length of the objective lens , we know from lens formula, $\dfrac{1}{u_{o}}+\dfrac{1}{v_{o}}=\dfrac{1}{f_{o}}$
$\implies \dfrac{1}{\dfrac{9}{5}}+\dfrac{1}{9}=\dfrac{1}{f_{o}}$
$\implies \dfrac{5}{9}+\dfrac{1}{9}=\dfrac{1}{f_{o}}$
$\implies \dfrac{6}{9}=\dfrac{1}{f_{o}}$
$\therefore \dfrac{1}{f_{o}}=3\;cm$
Hence we get that $f_{o}=3\;cm$ and $U_{O}=1.8\;cm \approx 2\;cm$

Thus, option $C. 3\; cm, 2 \;cm$ is the correct answer.

Additional Information:
Microscopes are used to magnify objects, the compound microscope has two convex lenses, namely the objective lens and the eyepiece. Both contribute to the final magnification. The objective lens produces a magnification value of about $5\times \; to \; 100\times$ the original size. The object is focused by adjusting the two lenses to produce an enlarged image. The object produces an image with certain magnification by the objective lens with $f_{o}$ , this image now acts a virtual object to the eyepiece with $f_{e}$ which in turn produces a virtual image, which is magnified further. The final image is generally inverted, and can be seen through the normal eyes.
Lens formula is the relationship between the distance of an object$u$, distance of image$v$ and the focal length of the lens$f$. This law can be used for both concave and convex lenses with appropriate sign conventions. The thickness of the lens is neglected.
Lens formula: $\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}$
And magnification equation is given by $M=\dfrac{Height\; of \;image}{Height\; of \;object}=- \dfrac{distance\; of\; image}{distance\; of\; object}$ if$M=+$ then the image is magnified and if $M=-$ then image is diminished.
But here since two lenses are used the magnification is given by $m=\dfrac{v_{o}}{u_{o}}\left(\dfrac{D}{f_{e}}\right)$.

Note:
The compound microscope has a pair of convex lenses, namely the objective lens and the eyepiece. Both contribute to the final magnification. The object produces an image with certain magnification by the objective lens with $f_{o}$ , this image now acts a virtual object to the eyepiece with $f_{e}$ which in turn produces a virtual image, which is magnified further.