Question

The length of a ballistic pendulum is 1 m and the mass of its block is 0.98kg. A bullet of mass 20g strikes the block along a horizontal direction and gets embedded in the block. If block $+$ bullet completes vertical circle of radius 1 m, the striking velocity of bullet is –

& \text{A) 280m}{{\text{s}}^{-1}} \\\ & \text{B) 350m}{{\text{s}}^{-1}} \\\ & \text{C) 420m}{{\text{s}}^{-1}} \\\ & \text{D) 490m}{{\text{s}}^{-1}} \\\ \end{aligned}$$

Answer 1

We need to understand the mechanical forces acting on the block when the bullet is hit on it. The velocity of the bullet along with its mass imparts a momentum on the block which can provide a centripetal force enough for both of them to undergo a circular motion.

Complete answer:
We are given a system of ballistic pendulum which has a block of mass M, when hit with a bullet of mass m undergoes a circular motion with radius r as shown below –

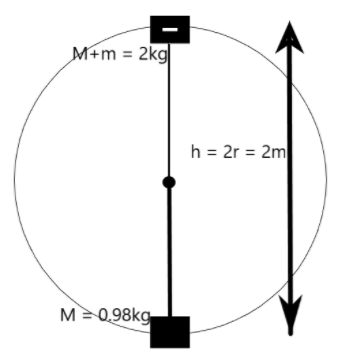
We can understand that a bullet when hit on the block of the ballistic pendulum will impart a momentum on the block which is completely transferred to it as the collision is completely inelastic and is along the horizontal.
We can use the conservation of linear momentum to equate them in both cases and find an expression for the velocity of the bullet.
According to the conservation of linear momentum –

& m{{v}_{i}}=(M+m){{v}_{f}} \\\ & \text{given,} \\\ & m=0.02kg \\\ & M=0.98kg \\\ & \Rightarrow (0.02){{v}_{i}}=(0.98+0.02){{v}_{f}} \\\ & 0.02{{v}_{i}}={{v}_{f}} \\\ & \therefore {{v}_{i}}=50{{v}_{f}}\text{ --(1)} \\\ \end{aligned}$$ We also know that the minimum kinetic energy is achieved when the object is at the maximum height, which can give the velocity at that point as – $$\begin{aligned} & K{{E}_{\min }}=P{{E}_{\max }} \\\ & \dfrac{1}{5}(M+m){{v}_{f}}^{2}=(M+m)gh \\\ & \therefore {{v}_{f}}=\sqrt{5gh} \\\ \end{aligned}$$ Now, we can consider the conservation of mechanical energy after the collision as this is an inelastic collision. We can consider the kinetic energy of the bullet is equal to the potential energy of the block-and-bullet system when at the maximum height. We can equate them as $$\begin{aligned} & \text{K}{{\text{E}}_{i}}+P{{E}_{i}}=K{{E}_{f}}+P{{E}_{f}} \\\ & \Rightarrow \dfrac{1}{2}m{{v}_{i}}^{2}+0=\dfrac{1}{2}(M+m){{v}_{f}}^{2}+(M+m)gh \\\ & (0.02){{v}_{i}}^{2}=(2){{(\sqrt{5gh})}^{2}}+2rg(2) \\\ & (0.02){{v}_{i}}^{2}=10g(2)+4g \\\ & (0.02){{v}_{i}}^{2}=24g \\\ & {{v}_{i}}^{2}=\dfrac{24g}{0.02} \\\ & \therefore {{v}_{i}}=346.4m{{s}^{-1}} \\\ \end{aligned}$$ The velocity of the bullet is approximately, $${{v}_{i}}=350m{{s}^{-1}}$$. **The correct answer is option B.** **Note:** We need to keep in mind that the kinetic energy has a non-zero minimum value defined at the maximum attained height for a vertical circular motion unlike the other oscillations and vibrations where the kinetic or potential energy completely oscillates between zero and maximum.