Question

The largest possible set of real number which can be the domain of $f(x)=\sqrt{1}-\left( \dfrac{1}{x} \right)$ is:
(1) $(0,1)\cup (0,\infty )$
(2) $(-1,0)\cup (1,\infty )$
(3) $(-\infty ,-1)\cup (0,\infty )$
(4) $(-\infty ,0)\cup [1,\infty )$

Answer 1

To solve this question you should know what is function, what is the domain and range of a function. Firstly we will see the equation given to us then we will see what we can input in the function remembering the conditions to be followed to find the domain.

Complete step by step answer:
A function is a relation where each input has a particular output. A function is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output.
Let A & B be any two two non empty sets from A to B , will be a function only when every element in set A has one and only one image in set B. Functions are generally represented as $f(x)$
For example: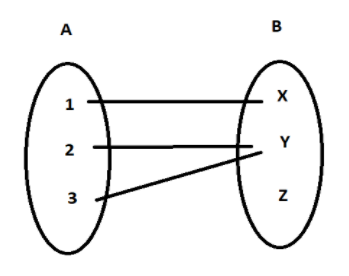
Domain is the set of all inputs for which the function is valid , whereas the range of a function is the set of outputs that the function will produce . We can also define domain and range as, domain is the set of numbers which are valid values for the independent variable. The range is the set of valid numbers for the dependent variable.
That is Domain = input =x
Range = output = y
Conditions to be remembered while finding the domain:
The denominator of a fraction cannot be zero.
The number under a square root sign must be positive.
So, according to the question we are given a equation that is
$1-\dfrac{1}{x}$
Now, to find the domain
1-\dfrac{1}{x}$$$$\ge $$$$0
\Rightarrow $$$$\dfrac{x-1}{x}$$$$\ge $$$$0
Now taking numerator and denominator and plotting it then we will get two points that is
$0$,$1$

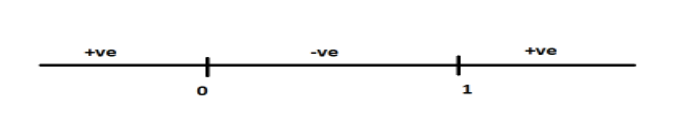
So, as we can see in the above figure, the numbers between $0$and $1$will give a negative value inside the root which is not valid.
So, the domain of the function is
$(-\infty ,0)\cup [1,\infty )$
$0$will not be the part of the domain as $0$in the denominator will give a invalid result.
Therefore $0$is excluded from the domain.
So, the correct answer is “Option 4”.

Note:
What can go into a function is called the Domain of a function. What may possibly come out of a function is referred to as the codomain of a function. What actually comes out of a function is called the range of a function. The range is a subset of the codomain. There should be no negative values inside the square root and no zero value in the denominator while finding the domain.