Question

The largest and the shortest distance of the earth from the sun is ${{r}_{1}}$ and ${{r}_{2}}$. Its distance from the sun when it is at perpendicular to the major axis of the orbit drawn from the sun is
$\begin{aligned} & \text{A}\text{. }\dfrac{{{r}_{1}}+{{r}_{2}}}{4} \\\ & \text{B}\text{. }\dfrac{{{r}_{1}}+{{r}_{2}}}{{{r}_{1}}-{{r}_{2}}} \\\ & \text{C}\text{. }\dfrac{2{{r}_{1}}{{r}_{2}}}{{{r}_{1}}+{{r}_{2}}} \\\ & \text{D}\text{. }\dfrac{{{r}_{1}}+{{r}_{2}}}{3} \\\ \end{aligned}$

Answer 1

The earth rotates around the sun in an elliptical orbit with the sun located at one of its foci. with the largest and the shortest distance of the earth from the sun is ${{r}_{1}}$ and ${{r}_{2}}$. The distance of Earth from the sun when the earth is at perpendicular to the major axis of the orbit drawn from the sun is half of the directrix. Directrix is related to semi major axis and semi minor axis. First write down ${{r}_{1}}$ and ${{r}_{2}}$ in terms of sum and product. Relate them with the directrix and take half of the directrix to get the perpendicular distance.

Formula used:
Consider an ellipse having semi major axis length $2a$, semi minor axis length $2b$, directrix $d$, eccentricity $e$. Then the directrix is given by $d=\dfrac{2{{b}^{2}}}{a}$.
Eccentricity is given by ${{e}^{2}}=1-\dfrac{{{b}^{2}}}{{{a}^{2}}}$
The perpendicular distance of directrix from the centre (where the semi major axis and semi minor axis meets) is $ae$
We have to calculate half of the directrix. i.e. $\dfrac{d}{2}$

Complete step-by-step answer:

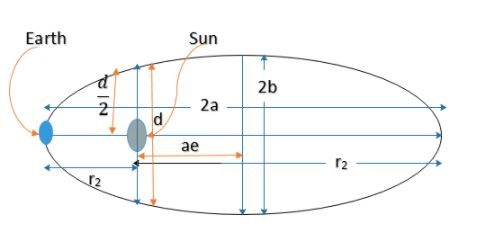
According to Kepler’s law of gravitation the earth rotates around the sun in an elliptical orbit with the sun situated in one of the foci of the orbit.
Let the earth rotate around the sun with an elliptical orbit with semi major axis length is $'2a'$ and semi minor axis length $'2b'$.
Then the length of the directrix is given by $d=\dfrac{2{{b}^{2}}}{a}$.
The distance of Earth from the sun when the earth is at perpendicular to the major axis of the orbit drawn from the sun is $\dfrac{d}{2}$. So We have to calculate the half of the directrix.
The perpendicular distance of the directrix from the centre (where the semi major axis and semi minor axis meets) is $ae$ where $e$ is the eccentricity of the ellipse.
According to question ${{r}_{1}}$ is the largest distance of earth from sun and ${{r}_{2}}$ is the shortest distance from earth from the sun.
So from figure
${{r}_{1}}=a+ae=a\left( 1+e \right)$ and
${{r}_{2}}=a-ae=a(1-e)$
Now
$\begin{aligned} & {{r}_{1}}+{{r}_{2}}=a+ae+a-ae=2a \\\ & \Rightarrow \dfrac{{{r}_{1}}+{{r}_{2}}}{2}=a \\\ \end{aligned}$
And , ${{r}_{1}}{{r}_{2}}=a\left( 1+e \right)a\left( 1-e \right)={{a}^{2}}\left( 1+e \right)\left( 1-e \right)={{a}^{2}}\left( 1-{{e}^{2}} \right)$
But for ellipse the relation between the eccentricity and semi major axis and semi minor axis is
${{e}^{2}}=1-\dfrac{{{b}^{2}}}{{{a}^{2}}}$
Putting it in above equation we get
$\begin{aligned} & {{r}_{1}}{{r}_{2}}={{a}^{2}}\left( 1-\left[ 1-\dfrac{{{a}^{2}}}{{{b}^{2}}} \right] \right)={{b}^{2}} \\\ & \Rightarrow {{r}_{1}}{{r}_{2}}={{b}^{2}} \\\ \end{aligned}$
Now the directrix is given by
$d=\dfrac{2{{b}^{2}}}{a}=\dfrac{2{{r}_{1}}{{r}_{2}}}{\left( \dfrac{{{r}_{1}}+{{r}_{2}}}{2} \right)}=\dfrac{4{{r}_{1}}{{r}_{2}}}{{{r}_{1}}+{{r}_{2}}}$
The distance of earth from the sun when the earth is at perpendicular to the major axis of the orbit drawn from the sun is
$\dfrac{d}{2}=\dfrac{\dfrac{4{{r}_{1}}{{r}_{2}}}{({{r}_{1}}+{{r}_{2}})}}{2}=\dfrac{2{{r}_{1}}{{r}_{2}}}{({{r}_{1}}+{{r}_{2}})}$
So the correct option is $\text{C}\text{. }\dfrac{2{{r}_{1}}{{r}_{2}}}{{{r}_{1}}+{{r}_{2}}}$

So, the correct answer is “Option C”.

Additional Information: Ellipse: It is a curve surrounding two points such that for all points on the curve the sum of the distances to the two fixed points is constant. The two fixed points are called focus of the ellipse.
An ellipse may also be defined in terms of one focus and a line outside of focus and directrix. If the directrix is situated at a distance $'c'$ from the centre of the ellipse. For all points on the ellipse the ratio of distance of the focus to the directrix is constant. This constant ratio is called eccentricity. So,
$e=\dfrac{c}{a}=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}}$

Note: The Kepler’s law of planetary motion is valid for every terrestrial object. Newton gave his law of gravitation on the basis of Kepler’s law of planetary motion. Newton gave the following conclusions.
(i)A planet is acted upon by centripetal force directed towards the sun.
(ii)the force acting on the planet is inversely proportional to the square of the distance between the planet and the sun.
(iii)The force acting upon a planet is directly proportional to the product of the masses of the planet and the sun.