Question

The kite string is $65m$ long and makes an angle of ${32^ \circ }$ with the ground. How do you calculate the vertical height of the kite to the nearest meter?

Answer 1

Hint : As we know that the above given question is a word problem. A problem is a mathematical question written as one sentence or more describing a real life scenario where that problem needs to be solved by the way of mathematical calculation. We can solve the given problem by applying the trigonometric function.

Complete step by step solution:
We need to first understand the requirement of the question which is the height of the kite. First we will draw a diagram according to the question and then we solve it.

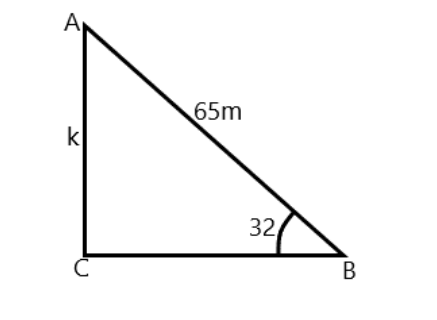
Here in the above figure let that $AC$ be the height of the kite i.e. $k$ . Now we know that $\angle CBA = {32^ \circ }$ . And ABC is a right angled triangle.
We know that $\sin \theta = \dfrac{p}{h}$ , and from the above figure we know that perpendicular is the height i.e. $k$ and hypotenuse is $AB = 65m$ and $\theta = 32$ .
Now applying the above formula we have $\sin 32 = \dfrac{k}{{65}}$ . We know that the decimal value of $\sin 32$ is $0.5299(approx)$ .
By substituting the above value we have
$0.5299 = \dfrac{k}{{65}} \Rightarrow k = 65 \times 0.5299 = 34.448$ .
Hence the required height of the kite is $34m(approx).$

Note : Before solving this kind of question we should have the proper knowledge of trigonometric functions and their values. We should note that the value of $\sin 32$ degree is the same as in $radian$ . To obtain the values in radian we need to multiply it with $\dfrac{\pi }{{180}}$ . So the sin of $32$ degrees is $0.5299$ , the same as of sin $32$ in radians.