Question

The kinetic energy of photoelectron emitted on irradiating a metal surface with frequency $\nu$ shows:
(A)- A straight line with slope equal to Planck’s constant.
(B)- A straight line with intercept on x-axis equal to the product of threshold frequency and Planck’s constant.
(C)-A straight line with extrapolated intercept on the y-axis equal to threshold energy.
(D)- A straight line with intercept on x-axis equal to threshold frequency.

Answer 1

From the photoelectric effect, it is seen that on irradiating the metal surface with EM radiations, the photons cause the electrons to ejects from the metal surface. Such that the energy given by the photon, is used in breaking the electron away from the surface known as the work function (binding energy). The remaining goes into the electron for its kinetic energy.

Complete step by step answer:
We have the Photoelectric effect equation given by:
${{E}_{radiation}}={{E}_{binding}}+K{{E}_{electron}}$
$hf=\phi +{{E}_{k}}$ , where h is the Planck’s constant and f is the frequency of the radiation, $\nu$.
In order to obtain a graph for kinetic energy versus the frequency of the radiation, the above equation can be rearranged to obtain the kinetic energy of the electron as follows:
${{E}_{K}}=hf-\phi$

On plotting the graph, between the Kinetic energy and frequency of the radiation, it is seen that a straight line is obtained which does not pass from the origin but at a certain distance.
Equating the above equation to the equation of straight line, y= mx + c. we have the dependent variable,$y={{E}_{K}}$ and the independent variable, $x=f$ , where m is the slope and c is the constant.

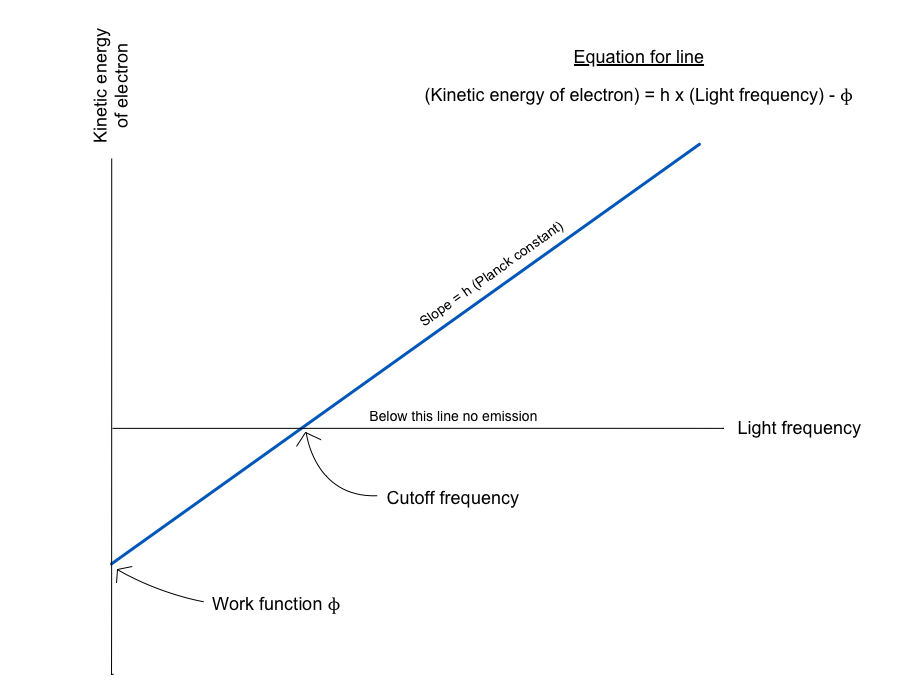
The slope of the line is equal to h (Planck’s constant) and the constant c is the intercept of the line as it is extrapolated to the Y-axis which is equal to $\phi$ (the binding energy or the threshold energy).
Also, the line on extrapolation intercepts the X-axis, giving the threshold frequency, which is the minimum energy required for the ejection of the electron.

Therefore, we have multiple correct options. That is option (A)- A straight line with slope equal to Planck’s constant.
(C)-A straight line with extrapolated intercept on the y-axis equal to threshold energy.
(D)- A straight line with intercept on x-axis equal to threshold frequency.
So, the correct answer is “Option A, C and D”.

Note: If the frequency of the photon is less than threshold frequency, then the electron will not be ejected. That is why the line does not pass from the origin.
Also, the work function is equivalent to the binding energy, as the work required to break away the electron from the surface.