Question

The kinetic energy $K$ of a particle moving along the x-axis varies with its position $\left( x \right)$ as shown in figure.

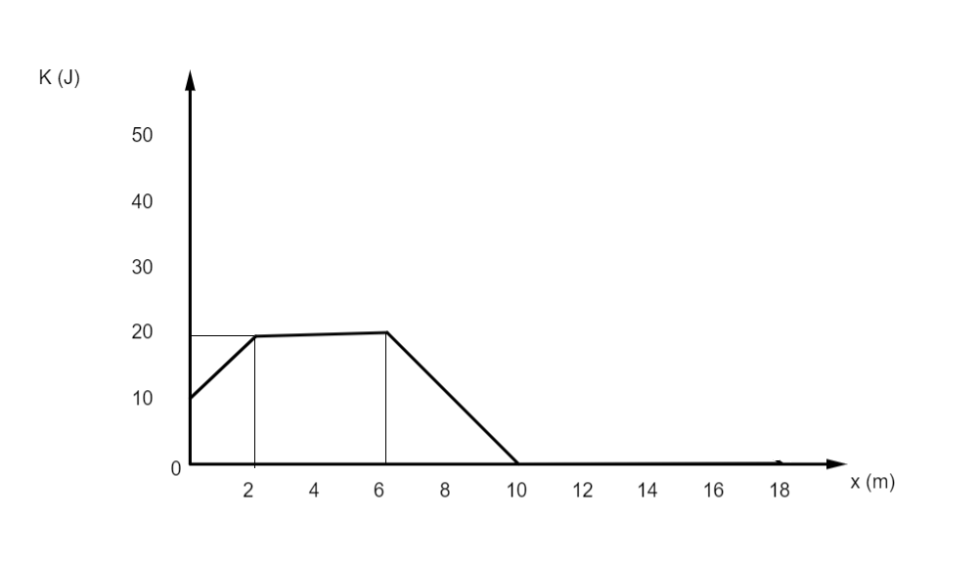
The magnitude of force acting on particle $x=9m$ is
$\begin{aligned} & A)0N \\\ & B)5N \\\ & C)20N \\\ & D)7.5N \\\ \end{aligned}$

Answer 1

Here, the given graph is plotted between kinetic energy and displacement. From the graph, it is clear that kinetic energy is changing with respect to the displacement. By work-energy theorem, change in kinetic energy is equal to the work done. From this concept, we can find force, as work done is equal to the dot product of force and displacement.
Formula used:
$\begin{aligned} & \Delta K=F.x \\\ & W=F.x \\\ \end{aligned}$

Complete answer:

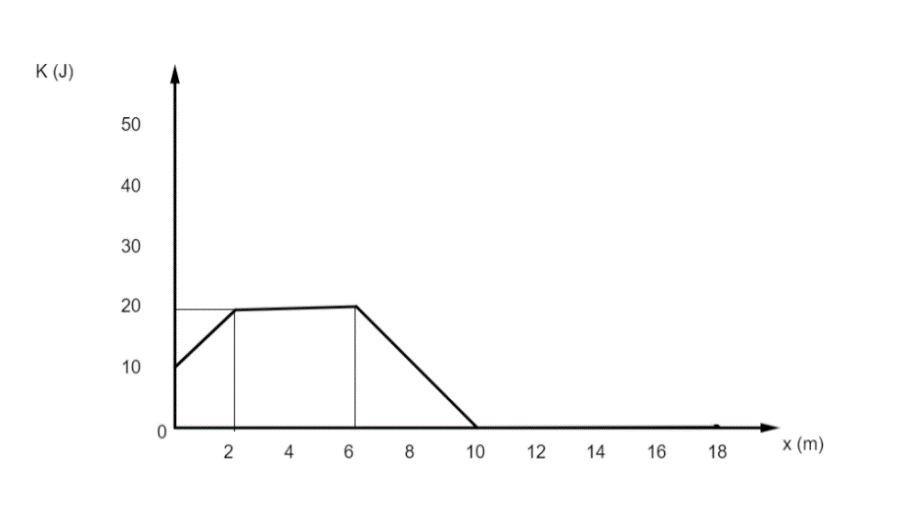
From the given plot between kinetic energy and displacement, it is clear that when the displacement is $9m$, the kinetic energy is in its way from its maximum value to zero. From the work-energy theorem, we know that the change in kinetic energy is converted as the work done. Therefore, we can write:
$\Delta K=W$
where
$\Delta K$ is the change in kinetic energy
$W$is the work done
Let this be equation 1.
We also know that work done is equal to the dot product of force and displacement. Therefore, we have
$W=F.x$
where
$F$is the force acting on the body
$x$ is the displacement caused due to this force
Let this be equation 2.
From equation 1 and equation 2, we have
$\Delta K=F.x\Rightarrow F=\dfrac{\Delta K}{x}$
Let this be equation 3.
Now, from the given graph, it is clear that $\dfrac{\Delta K}{x}$ gives the slope of the slanting region.
Hence, by finding the slope, we can find the force acting on a particular point.
Clearly, force can be expressed as
$F=slope=\dfrac{{{K}_{2}}-{{K}_{1}}}{{{x}_{1}}-{{x}_{2}}}$
where
${{K}_{1}}=0J$ is the minimum kinetic energy, as clear from the graph
${{K}_{2}}=20J$ is the maximum kinetic energy, as clear from the graph
${{x}_{1}}=10m$ is the displacement corresponding to the minimum kinetic energy, as clear from the graph
${{x}_{2}}=6m$ is the displacement corresponding to maximum kinetic energy, as clear from the graph
Let this be expression 4.
Solving expression 4 by substituting the values given in graph, we have
$\begin{aligned} & F=\dfrac{20J-0J}{10m-6m} \\\ & F=\dfrac{20J}{4m} \\\ & F=5N \\\ \end{aligned}$
Hence, force acting from $6m$ to $10m$ is $5N.$
Therefore, at $x=9m$, the force is $5N$ .

The correct answer is option $B$.

Note:
In the equation $F=\dfrac{\Delta K}{x}$, students might have a tendency to take the displacement at $9m$. But this is not right, as it needs to be understood that the slope at any point