Question

The kinetic energies of a planet in an elliptical orbit about the Sun, at positions A,B and C are ${{K}_{A}}$, ${{K}_{B}}$And ${{K}_{C}}$respectively. AC is the major axis and SB is perpendicular to AC at the position of the Sun S as shown in the figure. Then.

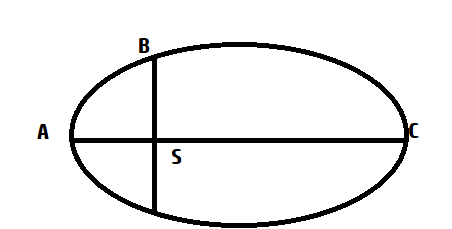
A- ${{K}_{B}}<{{K}_{A}}<{{K}_{C}}$
B- ${{K}_{A}}<{{K}_{B}}<{{K}_{C}}$
C- ${{K}_{B}}>{{K}_{A}}>{{K}_{C}}$
D- ${{K}_{A}}>{{K}_{B}}>{{K}_{C}}$

Answer 1

The problem involves the movement of planets around the sun. The motion of planets around the sun is because of the gravitational force and due to mutual gravitational forces, the planets move in such orbits without leaving the trajectory.

Complete step by step answer:
According to Kepler’s third law the square of the time period of the satellite is directly proportional to the third power of the radius of the orbit.
Also, from Kepler’s second law the areal velocity of the satellite remains constant. The planet moves in an elliptical orbit and its velocity will be maximum; its distance from the sun is minimum. This is evident from the equation: mvr= constant= angular momentum.

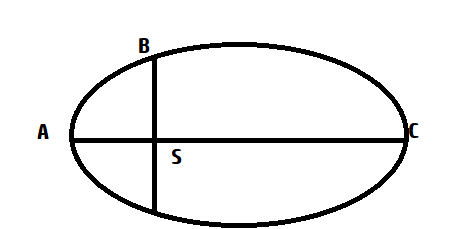
Since no external force acts on the system, angular momentum remains constant. Point A is perihelion and C is aphelion. Thus, ${{v}_{A}}>{{v}_{B}}>{{v}_{C}}$ and kinetic energy is directly proportional to the velocity.
Thus, ${{K}_{A}}>{{K}_{B}}>{{K}_{C}}$. So, the correct option is (D)

Note: When a planet orbits about the sum, the angular momentum of the planet about the sun remains conserved. Angular momentum conservation plays an important role in the movement of planets and other heavenly bodies. Both energy conservation and angular momentum conservation are important to planetary orbits.