Question

The ionization energy of the hydrogen atom is 13.6 eV. A hydrogen atom in the ground state is excited by the electromagnetic radiation of energy 12.1 eV. How many spectral lines will be emitted by the hydrogen atom?
(A). One
(B). Two
(C). Three
(D). Four

Answer 1

Hint: Here we first calculate the difference between the ionization energy and the radiation energy. Then using the formula $E = - \dfrac{{{E_0}}}{{{n^2}}}$ we can calculate the energy state in which the hydrogen atom is present after excitation which is coming as 3rd energy state. Then write all the possible transitions like $3^{rd}$ to $2^{nd}$, $2^{nd}$ to $1^{st}$, and $3^{rd}$ to $1^{st}$ which will give us 3 spectral lines.

Formula used: $E = - \dfrac{{{E_0}}}{{{n^2}}}$

Complete step-by-step solution -
Ionization energy denoted Eᵢ, is the minimum amount of energy required to remove the most loosely bound electron that is the valence electron, of an isolated neutral gaseous atom or molecule.
We know that the ionization energy of the hydrogen atom at the ground state is equal to -13.6 eV.
Now, this hydrogen atom is excited by electromagnetic energy equal to 12.1 eV.
So the energy difference is
$\Delta E = - 13.6 + 12.1 = - 1.5eV$------------------ (!)
that is the same as the energy of hydrogen atom in excited state
$E = - 1.5eV$----------------------------- (2)
Now we know that the energy level of hydrogen is given by the formula
$E = - \dfrac{{{E_0}}}{{{n^2}}}$------------------------------- (3)
Here ${E_0} = 13.6eV$ and $n = 0,1,2,3$ …and so on is the energy level where the atom is present.
Now equation (3) in equation (2) we will get
$\Rightarrow - 1.5 = - \dfrac{{13.6}}{{{n^2}}}$
$\Rightarrow {n^2} = \dfrac{{13.6}}{{1.5}} = 9.067$
$\Rightarrow n = \sqrt {9.067} \approx 3$

Therefore, Hydrogen is excited by radiation to the third energy state. Now the possible spectral lines that can be emitted are from $3^{rd}$ to $2^{nd}$, $2^{nd}$ to $1^{st}$, and $3^{rd}$ to $1^{st}$. Therefore 3 spectral lines will be emitted by the hydrogen atom as shown in figure 1. Hence, option C is correct.

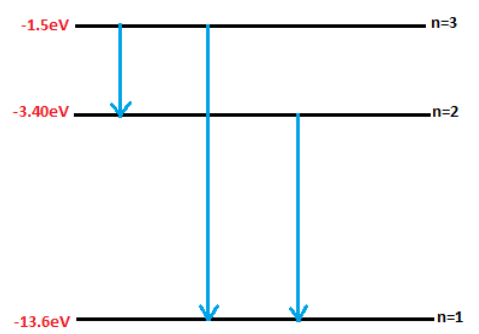
figure 1

Note: For these types of questions, we first find the energy difference ionization energy and radiation energy. Then recall the formula for the energy level of the atom which is $E = - \dfrac{{{E_0}}}{{{n^2}}}$, here ${E_0}$ is the ionization energy of the atom chosen. After that, we can simply solve for $n$ to get the energy state where the atom is present, and then by writing all the possible transitions from that state to lower state we will know the number of spectral lines.