Solveeit Logo
Login

Question

Question: The ionization constant of water at 27°C is $10^{-14}$ and at 77°C is $2 \times 10^{-14}$ $2H_2O (\...

The ionization constant of water at 27°C is 10−1410^{-14} and at 77°C is 2×10−142 \times 10^{-14}

2H2O(ℓ)⇌H3O+(aq)+OH−(aq)2H_2O (\ell) \rightleftharpoons H_3O^+ (aq) + OH^- (aq) [Take: In 2=0.7]

If magnitude of 'Δ\DeltaS' at 27°C is 'X' cal mol−1K−1mol^{-1} K^{-1}, then Find the value of (X10)(\frac{X}{10}) (Assume ΔionH\Delta_{ion}H is independent of temperature

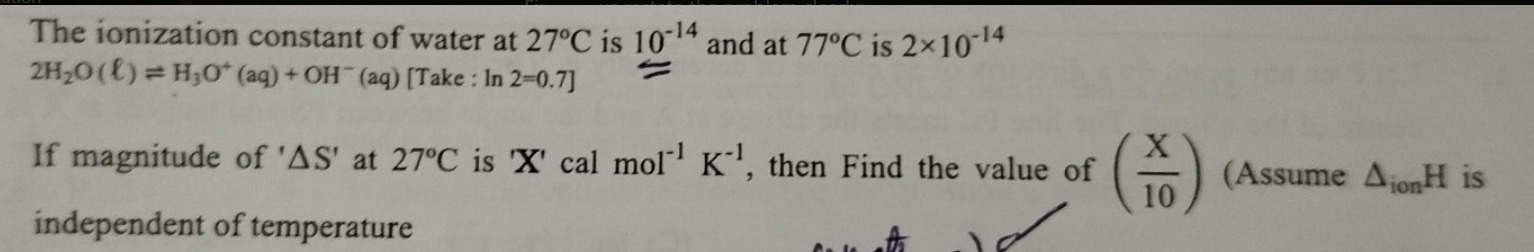
Answer

5.44

Explanation

Solution

Solution:

  1. The equilibrium constant at temperature T is related to ΔG:

    ΔG=ΔH−TΔS=−RTln⁡K.\Delta G = \Delta H - T\Delta S = -RT\ln K.

    Since ΔH is assumed independent of T, the temperature–variation of K gives:

    dln⁡KdT=ΔHRT2.\frac{d\ln K}{dT}=\frac{\Delta H}{RT^2}.

  2. For the two temperatures, we write:

    ln⁡K2−ln⁡K1=ΔHR(1T1−1T2),\ln K_2 - \ln K_1 = \frac{\Delta H}{R}\left(\frac{1}{T_1}-\frac{1}{T_2}\right),

    where

    K1=10−14 at T1=27∘C=300 K,K2=2×10−14 at T2=77∘C=350 K.K_1 = 10^{-14} \text{ at } T_1 = 27^\circ\text{C} = 300\,\text{K},\quad K_2=2\times10^{-14}\text{ at } T_2 = 77^\circ\text{C} = 350\,\text{K}.

    Compute the LHS:

    ln⁡K2−ln⁡K1=ln⁡(2×10−1410−14)=ln⁡2≈0.6931.\ln K_2 - \ln K_1 = \ln\left(\frac{2\times 10^{-14}}{10^{-14}}\right)=\ln2\approx 0.6931.

    And,

    1300−1350=350−300300×350=50105000≈0.00047619 K−1.\frac{1}{300}-\frac{1}{350} = \frac{350-300}{300\times350}=\frac{50}{105000}\approx0.00047619\,\text{K}^{-1}.

    Therefore,

    ΔH=R×0.69310.00047619.\Delta H = R\times\frac{0.6931}{0.00047619}.

    Taking R=1.987 cal mol−1K−1R = 1.987\,\text{cal\,mol}^{-1}\text{K}^{-1},

    ΔH≈1.987×0.69310.00047619≈2888 cal/mol.\Delta H \approx 1.987\times\frac{0.6931}{0.00047619}\approx 2888\,\text{cal/mol}.

  3. To find ΔS at 27°C (300 K), use the Gibbs relation:

    ΔH−TΔS=−RTln⁡K⟹ΔS=ΔH+RTln⁡KT.\Delta H - T\Delta S = -RT\ln K \quad\Longrightarrow\quad \Delta S = \frac{\Delta H + RT\ln K}{T}.

    For T=300 KT=300\,\text{K} and ln⁡(10−14)=−14ln⁡10≈−32.236\ln(10^{-14})=-14\ln10\approx -32.236:

    ΔS=2888+1.987×300×(−32.236)300.\Delta S = \frac{2888 + 1.987\times300\times(-32.236)}{300}.

    First, calculate:

    1.987×300≈596.1,596.1×(−32.236)≈−19200 cal/mol.1.987\times300\approx 596.1,\quad 596.1\times(-32.236)\approx -19200\,\text{cal/mol}.

    Then,

    ΔS=2888−19200300≈−16312300≈−54.37 cal mol−1K−1.\Delta S = \frac{2888-19200}{300} \approx \frac{-16312}{300}\approx -54.37\,\text{cal\,mol}^{-1}\text{K}^{-1}.

    The magnitude is ∣ΔS∣≈54.4 cal mol−1K−1|\Delta S|\approx 54.4\,\text{cal\,mol}^{-1}\text{K}^{-1}.

  4. Since the question defines this magnitude as XX and asks for X10\frac{X}{10},

    X10≈54.410≈5.44.\frac{X}{10}\approx \frac{54.4}{10}\approx 5.44.