Solveeit Logo
Login

Question

Question: The ionic equivalent conductivity of $C_2O_4^{-2}$, $K^+$ and $Na^+$ ions are $x, y, z \ S \ cm^2 \ ...

The ionic equivalent conductivity of C2O4−2C_2O_4^{-2}, K+K^+ and Na+Na^+ ions are x,y,z S cm2 eq−1x, y, z \ S \ cm^2 \ eq^{-1} respectively. Then, Λeq∘\Lambda_{eq}^{\circ} of (NaOOC−COOK)(NaOOC-COOK) is

A

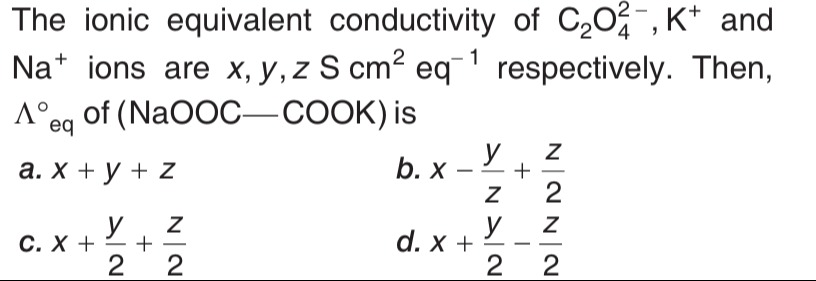
x+y+zx + y + z

B

x−yz+z2x - \frac{y}{z} + \frac{z}{2}

C

x+y2+z2x + \frac{y}{2} + \frac{z}{2}

D

x+y2−z2x + \frac{y}{2} - \frac{z}{2}

Answer

x+y2+z2x + \frac{y}{2} + \frac{z}{2}

Explanation

Solution

The salt is (NaOOC−COOK)(NaOOC-COOK), which is Potassium Sodium Oxalate, with the chemical formula NaKC2O4NaKC_2O_4. When this salt dissolves in water, it dissociates into ions:

NaKC2O4→Na++K++C2O42−NaKC_2O_4 \rightarrow Na^+ + K^+ + C_2O_4^{2-}

According to Kohlrausch's Law of Independent Migration of Ions, the equivalent conductivity of an electrolyte at infinite dilution (Λeq∘\Lambda_{eq}^{\circ}) is the sum of the equivalent conductivities of the ions produced by one equivalent of the electrolyte.

Λeq∘(electrolyte)=∑(number of equivalents of ion per equivalent of electrolyte)×λeq∘(ion)\Lambda_{eq}^{\circ}(\text{electrolyte}) = \sum (\text{number of equivalents of ion per equivalent of electrolyte}) \times \lambda_{eq}^{\circ}(\text{ion})

Alternatively, and more commonly applied:

Λeq∘(electrolyte)=λeq∘(total cations)+λeq∘(total anions)\Lambda_{eq}^{\circ}(\text{electrolyte}) = \lambda_{eq}^{\circ}(\text{total cations}) + \lambda_{eq}^{\circ}(\text{total anions})

where λeq∘(total cations)\lambda_{eq}^{\circ}(\text{total cations}) is the sum of the equivalent conductivities of all cations produced from one equivalent of the electrolyte, and similarly for anions.

Given:

  • λeq∘(C2O4−2)=x S cm2 eq−1\lambda_{eq}^{\circ}(C_2O_4^{-2}) = x \ S \ cm^2 \ eq^{-1}

  • λeq∘(K+)=y S cm2 eq−1\lambda_{eq}^{\circ}(K^+) = y \ S \ cm^2 \ eq^{-1}

  • λeq∘(Na+)=z S cm2 eq−1\lambda_{eq}^{\circ}(Na^+) = z \ S \ cm^2 \ eq^{-1}

Applying Kohlrausch's Law:

Λm∘(NaKC2O4)=λm∘(Na+)+λm∘(K+)+λm∘(C2O42−)\Lambda_m^{\circ}(NaKC_2O_4) = \lambda_m^{\circ}(Na^+) + \lambda_m^{\circ}(K^+) + \lambda_m^{\circ}(C_2O_4^{2-})

Using λm∘(Izi)=∣zi∣λeq∘(Izi)\lambda_m^{\circ}(I^{z_i}) = |z_i| \lambda_{eq}^{\circ}(I^{z_i}):

λm∘(Na+)=1×z=z\lambda_m^{\circ}(Na^+) = 1 \times z = z

λm∘(K+)=1×y=y\lambda_m^{\circ}(K^+) = 1 \times y = y

λm∘(C2O42−)=2×x=2x\lambda_m^{\circ}(C_2O_4^{2-}) = 2 \times x = 2x

Λm∘(NaKC2O4)=z+y+2x\Lambda_m^{\circ}(NaKC_2O_4) = z + y + 2x

The relationship between molar and equivalent conductivity is Λm∘=zΛeq∘\Lambda_m^{\circ} = z \Lambda_{eq}^{\circ}, where zz is the total charge per formula unit. For NaKC2O4NaKC_2O_4, z=2z=2.

Λeq∘(NaKC2O4)=Λm∘(NaKC2O4)2=z+y+2x2=z2+y2+x\Lambda_{eq}^{\circ}(NaKC_2O_4) = \frac{\Lambda_m^{\circ}(NaKC_2O_4)}{2} = \frac{z + y + 2x}{2} = \frac{z}{2} + \frac{y}{2} + x

Λeq∘(NaKC2O4)=x+y2+z2\Lambda_{eq}^{\circ}(NaKC_2O_4) = x + \frac{y}{2} + \frac{z}{2}