Question

The internal center of similitude of two circles ${{(x-3)}^{2}}+{{(y-2)}^{2}}=9,{{(x+5)}^{2}}+{{(y+6)}^{2}}=9$ is

& \text{(A) (-1,-2)} \\\ & \text{(B) (-2,-1)} \\\ & \text{(C) (3,2)} \\\ & \text{(D) (-5,-6)} \\\ \end{aligned}$$

Answer 1

Hint : We know that if $P({{x}_{1}},{{y}_{1}})$ and $Q({{x}_{2}},{{y}_{2}})$ are divided by $R({{x}_{3}},{{y}_{3}})$ in the ratio $m:n$ internally if ${{x}_{3}}=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},{{y}_{3}}=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n}$. We should know that if the internal centre of similitude of two circles ${{(x-{{x}_{1}})}^{2}}+{{(y-{{y}_{1}})}^{2}}=r_{1}^{2},{{(x-{{x}_{2}})}^{2}}+{{(y-{{y}_{2}})}^{2}}=r_{2}^{2}$ is $A({{x}_{3}},{{y}_{3}})$, then $A({{x}_{3}},{{y}_{3}})$ divides the centre of two circles in the ratio ${{r}_{1}}:{{r}_{2}}$. By using this concept, we can find the internal centre of similitude of ${{(x-3)}^{2}}+{{(y-2)}^{2}}=9,{{(x+5)}^{2}}+{{(y+6)}^{2}}=9$.

Complete step by step solution :
We know that if the internal centre of similitude of two circles ${{(x-{{x}_{1}})}^{2}}+{{(y-{{y}_{1}})}^{2}}=r_{1}^{2},{{(x-{{x}_{2}})}^{2}}+{{(y-{{y}_{2}})}^{2}}=r_{2}^{2}$ is $A({{x}_{3}},{{y}_{3}})$, then $A({{x}_{3}},{{y}_{3}})$ divides the centre of two circles in the ratio ${{r}_{1}}:{{r}_{2}}$ .

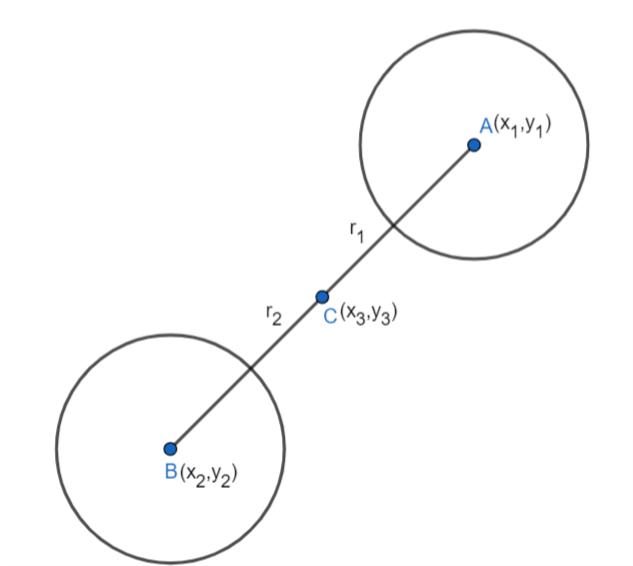
In the question, we were given two circles ${{(x-3)}^{2}}+{{(y-2)}^{2}}=9,{{(x+5)}^{2}}+{{(y+6)}^{2}}=9$.
Now let us compare ${{(x-3)}^{2}}+{{(y-2)}^{2}}=9$ with ${{(x-{{x}_{1}})}^{2}}+{{(y-{{y}_{1}})}^{2}}=r_{1}^{2}$.
We get

& {{x}_{1}}=3....(1) \\\ & {{y}_{1}}=2.....(2) \\\ & {{r}_{1}}^{2}=9 \\\ & \Rightarrow {{r}_{1}}=3....(3) \\\ \end{aligned}$$ Now let us compare $${{(x+5)}^{2}}+{{(y+6)}^{2}}=9$$ with $${{(x-{{x}_{2}})}^{2}}+{{(y-{{y}_{2}})}^{2}}=r_{2}^{2}$$. We get $$\begin{aligned} & {{x}_{2}}=-5...(4) \\\ & {{y}_{2}}=-6.....(5) \\\ & {{r}_{2}}^{2}=9 \\\ & \Rightarrow {{r}_{2}}=3....(6) \\\ \end{aligned}$$ We know that the internal centre of similitude divides the line joining the centre in the ratio $${{r}_{1}}:{{r}_{2}}$$ internally. So, we get the centre of $${{(x-3)}^{2}}+{{(y-2)}^{2}}=9$$ is $${{C}_{1}}(3,2)$$ and radius of $${{(x-3)}^{2}}+{{(y-2)}^{2}}=9$$ is equal to 3. In the similar manner, we get centre of $${{(x+5)}^{2}}+{{(y+6)}^{2}}=9$$ is $${{C}_{2}}(-5,-6)$$ and radius of $${{(x+5)}^{2}}+{{(y+6)}^{2}}=9$$ is equal to 3. So, it is clear that $$A({{x}_{3}},{{y}_{3}})$$ divides $${{C}_{1}}(3,2)$$ and $${{C}_{2}}(-5,-6)$$ in the ratio $$3:3$$ internally. We know that if $$P({{x}_{1}},{{y}_{1}})$$ and $$Q({{x}_{2}},{{y}_{2}})$$ are divided by $$R({{x}_{3}},{{y}_{3}})$$ in the ratio $$m:n$$ internally if $${{x}_{3}}=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},{{y}_{3}}=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n}$$. By using this concept, we get $$\begin{aligned} & \Rightarrow {{x}_{3}}=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n} \\\ & \Rightarrow {{x}_{3}}=\dfrac{3(-5)+3(3)}{3+3} \\\ & \Rightarrow {{x}_{3}}=-1.....(7) \\\ \end{aligned}$$ In the similar way, we get $$\begin{aligned} & \Rightarrow {{y}_{3}}=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \\\ & \Rightarrow {{y}_{3}}=\dfrac{3(-6)+3(2)}{3+3} \\\ & \Rightarrow {{y}_{3}}=-2.....(8) \\\ \end{aligned}$$ From equation (7) and equation (8), we get the coordinates of internal centre of similitude is $$(-1,-2)$$. Hence, option A is correct. **Note** : Some students have a misconception that if $$P({{x}_{1}},{{y}_{1}})$$ and $$Q({{x}_{2}},{{y}_{2}})$$ are divided by $$R({{x}_{3}},{{y}_{3}})$$ in the ratio $$m:n$$ internally if $${{x}_{3}}=\dfrac{m{{x}_{2}}-n{{x}_{1}}}{m-n},{{y}_{3}}=\dfrac{m{{y}_{2}}-n{{y}_{1}}}{m-n}$$. But we know that the given coordinates are the coordinates obtained if $$R({{x}_{3}},{{y}_{3}})$$ is get divided in the ratio $$m:n$$ externally. But if this misconception is followed, then we will get the external centre of similitude. But we want internal central similitude. So, this misconception hasto be avoided.