Question
Question: The intensity, at the central maxima (O) in a Young’s double slit set up is \({I_0}.\) If the distan...
The intensity, at the central maxima (O) in a Young’s double slit set up is I0. If the distance OP equals one third of the fringe width of the pattern, show that the intensity, at point P, would equal I2/4.
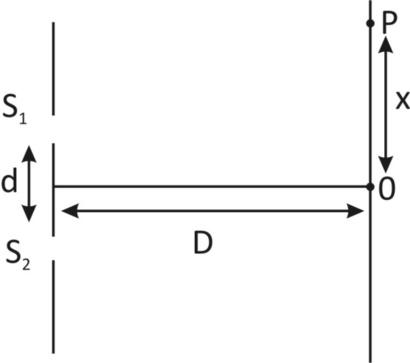
Solution
Concept of Young’s double slit experiment and the variation of intensity from central maximum to decreasing values as we go away from centre O. Also the lights entering from slits are from the same source , so the intensity at both slits are taken the same.
Formula used:
1. β=dλD
2. Path difference =λ2π×phase differences
φ=λ2π×Path differences
Complete step by step answer:
In the question the intensity at central maxima is I0. and we know that maximum intensity is given by
Imax=I0=(I1+I2)2Where I1 and I2respectively.
Here, I1=I2=I (say)
So, maximum intensity becomes,
I0=(I+I)2
I0=(2I)2
I0=4I.........(1)
Now, intensity at point P which is at a distance of x from O us given by
Ip=(I2+I2+2I1I2cosϕ)
Where φis the phase difference between two waves.
Since, I1=I2=I
So, IP=(I+I2+2I1cosϕ)
=(2I+2Icosϕ)
=2I(I+cosϕ)
=2I×2cos2ϕ/2 (as I+cosϕ=2cos22ϕ)
IP=4Icos22ϕ........(2)
From (1) and (2), we have
IP=I0cos22ϕ
Now, according to question, distance OP us one-third of the fringe width i.e. x=31β
Where β is fringe width
Now, we know that fringe width is given by β=αλD
So, distance OP becomes,
x=31β=31×dλD
x=3dλD and we know that path difference and phase difference are related as 2π×phase difference =α×path difference
⇒d=λ2π×Dxd
⇒d=λ2π×3dλD×Dd
⇒ϕ=32π........(3)
Put equation (3) in equation(2), we get
I=I0cos2232π
I=I0cos2(3π)
I=I0(21)2
I=4I0
Hence Proved.
Note:
Remember that for the same source I1=I2and for different sources I1=I2 and the also remember that with change in path length there is corresponding change in phase also.
