Question
Question: The integral $\int_0^\pi \frac{8xdx}{4\cos^2x + \sin^2x}$ is equal to...
The integral ∫0π4cos2x+sin2x8xdx is equal to
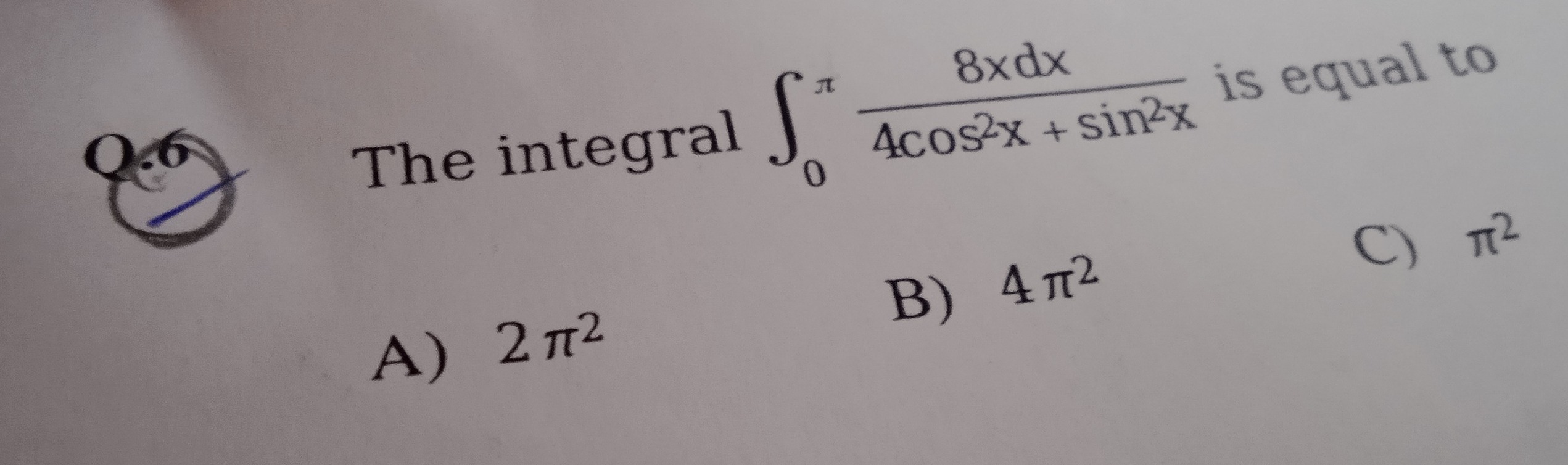
2π2
4π2
π2
2\pi^2
Solution
The integral to be evaluated is I=∫0π4cos2x+sin2x8xdx.
Step 1: Apply the property of definite integrals ∫0af(x)dx=∫0af(a−x)dx.
Let the given integral be I. Here, a=π.
I=∫0π4cos2(π−x)+sin2(π−x)8(π−x)dx
Since cos(π−x)=−cosx and sin(π−x)=sinx, we have cos2(π−x)=cos2x and sin2(π−x)=sin2x.
So, I=∫0π4cos2x+sin2x8(π−x)dx
Step 2: Add the original integral and the transformed integral.
Adding the original integral I=∫0π4cos2x+sin2x8xdx to the transformed integral:
2I=∫0π4cos2x+sin2x8xdx+∫0π4cos2x+sin2x8(π−x)dx
2I=∫0π4cos2x+sin2x8x+8(π−x)dx
2I=∫0π4cos2x+sin2x8x+8π−8xdx
2I=∫0π4cos2x+sin2x8πdx
2I=8π∫0π4cos2x+sin2xdx
I=4π∫0π4cos2x+sin2xdx
Step 3: Evaluate the new integral J=∫0π4cos2x+sin2xdx.
Let f(x)=4cos2x+sin2x1. We observe that f(π−x)=4cos2(π−x)+sin2(π−x)1=4cos2x+sin2x1=f(x).
This allows us to use the property ∫02af(x)dx=2∫0af(x)dx where 2a=π, so a=π/2.
J=2∫0π/24cos2x+sin2xdx
Step 4: Simplify the integrand by dividing the numerator and denominator by cos2x.
J=2∫0π/2cos2x4cos2x+cos2xsin2xcos2x1dx
J=2∫0π/24+tan2xsec2xdx
Step 5: Use substitution to evaluate the integral.
Let t=tanx. Then dt=sec2xdx.
When x=0, t=tan0=0.
When x=π/2, t=tan(π/2)→∞.
J=2∫0∞4+t2dt
This is a standard integral of the form ∫a2+x2dx=a1arctan(ax). Here a2=4, so a=2.
J=2[21arctan(2t)]0∞
J=[arctan(2t)]0∞
J=limt→∞arctan(2t)−arctan(20)
J=2π−0
J=2π
Step 6: Substitute the value of J back into the expression for I.
I=4πJ
I=4π(2π)
I=2π2
The final answer is 2π2.
