Question

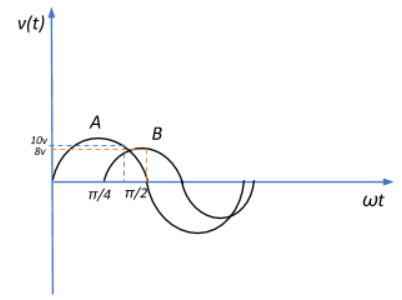
The instantaneous value at the $90^{\circ}$ point on the x-axis of the sine wave B shown in the figure is:

Answer 1

Notice that sine wave B lags with respect to sine wave A sine wave B begins a bit after wave A has already progressed. Determine this phase difference and substitute this in the sine wave equation to arrive at the appropriate instantaneous value.

Formula Used:
Sine wave instantaneous value $v = v_0sin(\omega t)$

Complete answer:
Let us begin by simply looking at the two waves exhibiting a sinusoidal variation as shown in the figure, with characteristic values along the y-axis and the phase angle along the x-axis

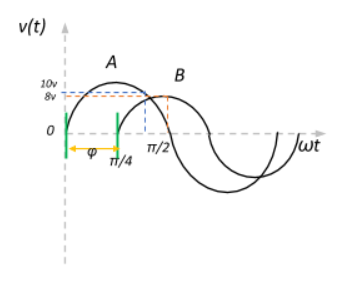
We have sine wave A starting at 0 and sine wave B starting at $\dfrac{\pi}{4}$ along the horizontal axis. We see that the start of sine wave B coincides with the peak of sine wave A at $\omega t = \dfrac{\pi}{4}$. This means that sine wave B is ahead in phase angle relative to sine wave A by a difference of $\phi = \dfrac{\pi}{4}$. We also see that the peak value of B coincides with the $\dfrac{\pi}{2}$ phase mark of wave A. Let us look at how the previous deductions would define the sinusoidal waves.
The general equation of a sine wave is given as:
$v(t)=v_0sin(\omega t)$, where v(t) is an instantaneous value, $v_0$ is the peak value $\omega$ is the angular frequency and t is the time, and $\omega t$ together form the phase angle of the wave.
Now, if the equation for sinusoidal wave A can generally be given as: $v(t) = v_0sin(\omega t)$, then the equation for sinusoidal wave B while accounting for the phase difference of $\phi$ will be given as:
$v(t) = v_0sin(\omega t+\phi)$
We can now find the instantaneous value at the $90^{\circ}$ point on the x-axis of the sine wave B.
From the diagram we see that for sine wave B at $\omega t = \dfrac{\pi}{2}$: $v_0 = 8v$, and equivalent phase angle $(\omega t+\phi) = (\dfrac{\pi}{2} + \dfrac{\pi}{4})$.
$\Rightarrow v(t) = 8vsin(\dfrac{\pi}{2} + \dfrac{\pi}{4})$
We know that $sin(\dfrac{\pi}{2} + \dfrac{\pi}{4})= cos\dfrac{\pi}{4} = cos\;45^{\circ} = \dfrac{1}{\sqrt{2}}$
Plugging this back into our equation we get:
$v(t) = 8vcos\;45^{\circ} = 8v \times \dfrac{1}{\sqrt{2}} = \dfrac{8v}{\sqrt{2}} = \dfrac{8v}{1.414} = 5.6568v$
Therefore, the instantaneous value at the $90^{\circ}$ point on the x-axis of the sine wave B is $\approx 5.66v$

Note:
Remember that the phase or phase angle of a periodic function such as the sine wave represents the point in time where the wave is in a cycle. Any sine wave that does not pass through zero at t=0 has a phase shift, as we’ve seen in the question. It essentially denotes the delay between two waves that have the same period or frequency. Just like phase, phase shift is also expressed in degrees or radians.