Question

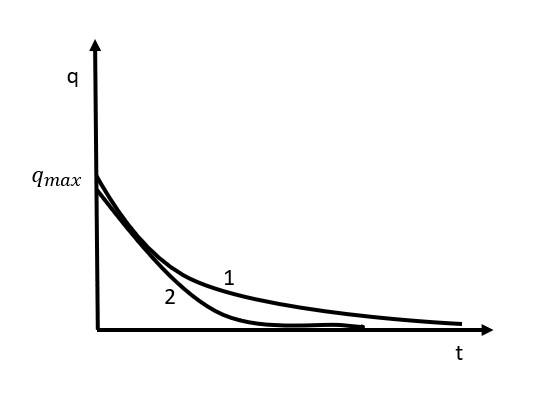
The instantaneous charge on a capacitor in two discharging RC circuits is plotted with respect to time in figure. Choose the correct statement (s) (where $E_{1}$ and $E_{2}$ are emfs of two DC sources in two different charging circuits and capacitors are fully charged).
a) $R_{1} C_{1} \gt R_{2} C_{2}$
b) $\dfrac{ R_{1} }{ R_{2} } \lt \dfrac{ C_{2}}{ C_{1}}$
c) $R_{1} \gt R_{2}$ if $E_{1} = E_{2}$
d) $C_{2} \gt C_{1}$ if $E_{1} = E_{2}$

Answer 1

Capacitor is discharging means the capacitor is giving up the charge that is stored in it. Hence, the capacitor's current exponentially reaches zero from its initial value, and the voltage of the capacitor goes exponentially to zero from its initial value. The time constant for RC circuit is -$\tau =RC$. During discharging, current will flow opposite to that of charging current i.e., from a negative terminal to positive terminal of the battery.

Complete step-by-step solution:
Both curves represent discharging of a capacitor.
If we see the graph, then the curve $1$ is steeper (approaching a straight line).
So, the slope of curve $1$ is more than curve$2$. Therefore, the time constant for $1$ is more than the curve $2$.
Time constant for RC circuit is-
$\tau =RC$.
It is known from the graph –
$\tau_{1} \gt \tau_{2}$
$\implies R_{1} C_{1} \gt R_{2} C_{2}$
$\implies \dfrac{ R_{1} }{ R_{2} } \gt \dfrac{ C_{2}}{ C_{1}}$
Time constant for curve 1 is more than the curve 2 .
$R_{1} \gt R_{2}$ and $C_{1} \gt C_{2}$
So, option (a, c) is correct.
Additional Information: - During the discharging of a capacitor, large current flows immediately, the voltage across the capacitor plates decreases as the charges move away from the plate. The current drops as less charges are repelling each other during the discharging.

Note: A charge can be charged gradually to the voltage and then discharged immediately to give the energy needed. The discharging current drops from an initial value, the potential difference over the capacitor plates lowers to zero when the capacitor is fully discharged.