Question

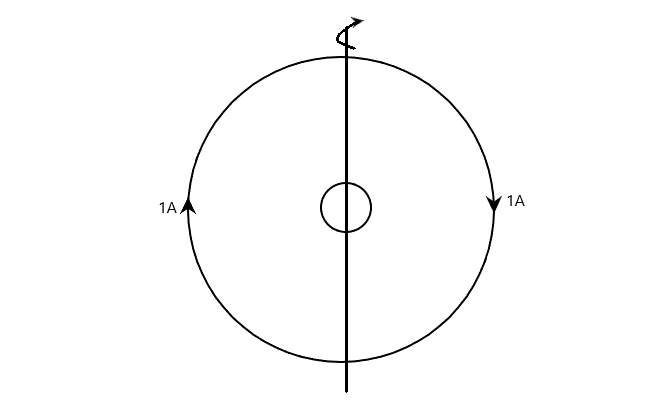
The inner loop has an area of $5 \times {10^{ - 4}}{m^2}$ and a resistance of $2\Omega$ (figure). The larger circular loop is fixed and has a radius of $0.1m$. Both the loops are concentric and coplanar. The smaller loop is rotated with an angular velocity $\omega$ rad/s about its diameter. The magnetic flux with the smaller loop is

A. $2\pi \times {10^{ - 6}}Wb$
B. $\pi \times {10^{ - 9}}Wb$
C. $\pi \times {10^{ - 9}}\cos \omega tWb$
D. Zero

Answer 1

The large fixed loop of wire can be regarded as a circular current loop. Hence, its magnetic field will be directed into the page at the centre of the circular turn.

Formula used: In this solution we will be using the following formulae;
$\phi = BA\cos \theta$ where $\phi$ is the magnetic flux passing through a loop of wire, $B$ is the magnetic field passing through the loop of wire, and $A$ is the area covered by the wire and $\theta$ is the angle between the area vector and the magnetic field.
$B = \dfrac{{\mu I}}{{2R}}$ where $B$ is the magnetic field of a circular current loop, $I$ is the current, and $R$ is the radius of the loop.
$\theta = \omega t$ where $\theta$ is the angle subtended, $\omega$ is the angular velocity, and $t$ is the time elapsed.

Complete step by step answer:
To solve the above, we note that the magnetic field generated by the current flowing the larger loop will cause a magnetic flux through the smaller rotating loop at the centre.
Now, the flux passing through the area (such as the one enclosed by a wire) can be given as
$\phi = BA\cos \theta$ where is the magnetic field passing through the loop of wire, and $A$ is the area covered by the wire and $\theta$ is the angle between the area vector and the magnetic field.
But the magnetic field is due to the larger loop, which is given as
$B = \dfrac{{\mu I}}{{2R}}$ where $B$ is the magnetic field of a circular current loop, $I$ is the current, and $R$ is the radius of the loop. Hence, the flux through the smaller loop is
$\phi = \dfrac{{\mu I}}{{2R}}A\cos \theta$ where $\theta = \omega t$ where $\theta$ is the angle subtended, $\omega$ is the angular velocity, and $t$ is the time elapsed.
Inserting all known values,
$\phi = \dfrac{{4\pi \times {{10}^{ - 7}}\left( 1 \right)}}{{2\left( {0.1} \right)}}\left( {5 \times {{10}^{ - 4}}} \right)\cos \omega t = \pi \times {10^{ - 9}}\cos \omega tWb$
Hence, the correct answer option C.

Note: Alternatively, if one remembers that since the smaller loop of wire is rotating, the flux through it has to be changing (since the larger one is not rotating along with it) we can simply know that option C is correct without calculating since all others imply a constant flux.