Question

The inductance of a coil is $L=10H$ and resistance $R=5\Omega$. If the applied voltage of the battery is 10V and it switches off at 1 millisecond, find the induced electromotive force of the inductor.

& \text{A}\text{. }2\times {{10}^{4}}V \\\ & \text{B}\text{. }1.2\times {{10}^{4}}V \\\ & \text{C}\text{. }2\times {{10}^{-4}}V \\\ & \text{D}\text{. None of these} \\\ \end{aligned}$$

Answer 1

The battery does work against the induced emf to develop the current and hence flux and that means flux will be proportional to current, which can be given as product of L and I where L will be inductance. And the induced emf is given as rate of change of flux with respect to time. By measuring flux we can measure the induced electromotive force of the inductor.

Formula used:

& \phi =LI \\\ & V=IR \\\ & \varepsilon =-\dfrac{d\phi }{dt} \\\ \end{aligned}$$ **Complete step by step answer:** The battery will have flux in order to oppose the induced emf and to flow current through it, which can be given by the following expression $$\phi =LI$$ Where ϕ is the flux, L is the inductance and I is the current. We can draw a circuit diagram for the given question as follows 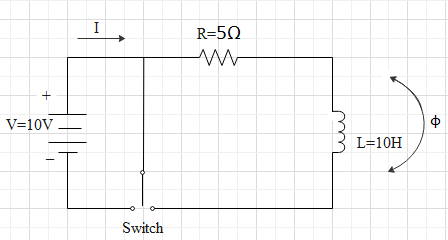 Now we have given voltage of battery and the resistance and by using Ohm’s law we can find current, which is given as $$\begin{aligned} & V=IR \\\ & I=\dfrac{V}{R} \\\ \end{aligned}$$ Substituting given values of V and R, $$V=10V\text{ and }R=5\Omega $$, we get $$\begin{aligned} & I=\dfrac{10}{5} \\\ & I=2A \\\ \end{aligned}$$ Hence current through the battery will be 2A. Now according to Faraday’s law of induction, induced electromotive force (emf) is proportional to the rate of change of flux linked with that coil and it is given as $$\varepsilon =-\dfrac{d\phi }{dt}$$ Negative sign indicates that the induced emf opposes the change in flux. We can further solve the Faraday’s law as follows: $$\begin{aligned} & \varepsilon =-\dfrac{d(LI)}{dt} \\\ & \varepsilon =-L\dfrac{dI}{dt} \\\ \end{aligned}$$ As per question, $$L=10H\text{ and }dt=1\text{millisecond=1}\times \text{1}{{\text{0}}^{-3}}s$$and the flow of current for this time interval will be 2A , therefore we can write $$dI=2A$$. Substituting given value in the above equation, we get $$\begin{aligned} & \varepsilon =-(10)\dfrac{(2)}{(1\times {{10}^{-3}})} \\\ & \varepsilon =-20\times {{10}^{3}}V \\\ & \varepsilon =-2\times {{10}^{4}}V \\\ \end{aligned}$$ The negative sign shows the direction as it opposes the change in flux or the flow of current, hence $$\varepsilon =2\times {{10}^{4}}V$$. **So, the correct answer is “Option A”.** **Note:** Here the inductance produced in the coil is the self-inductance as the induced emf of the coil is due the change in current in the same coil, in case there were two coils and an induced emf was produced due to change in current in other coil then it will give us mutual inductance. Also before substituting values the unit should be changed properly here we have changed millisecond into second to avoid error.